Análise combinatória (P.F.C)

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Análise combinatória (P.F.C)

Regras do fórum
Responder

Análise combinatória (P.F.C)

Mensagempor DanielRJ » Ter Ago 24, 2010 13:07

Olá pessoal tenho duvidas sobre exercicios meu objetivo é sanar todas essas duvidas mas é somente uma por topico então vamos devagar!

(AFA) A quantidade de numeros naturais de 4 algarismos distintos que podem ser formados por 1.2.3.4.5 e 6, que contém o algarismo 3 ou 4 é?
a)196
b)286
c)336
d)446
Avatar do usuário
DanielRJ
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 254
Registrado em: Sex Ago 20, 2010 18:19
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo

Re: Análise combinatória (P.F.C)

Mensagempor alexandre32100 » Ter Ago 24, 2010 15:24

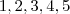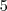Pra começar você deve definir a quantidade de números de quatro algarismos distintos com os números 1, 2, 3, 4, 5 e 6, sem se importar se há ou não um 3 ou 4 entre eles, que é 6\times5\times4\times3 (6 escolhas possíveis para o primeiro algarismo, 5 escolhas para o segundo, 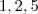4 para o terceiro e 3 para o quarto).
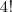Depois, deve excluir deste total os números que não possuem nem o 3, nem o 4. Estes número são formados apenas pelos algarismo 1,2,5 e 6, totalizando 4! possibilidades.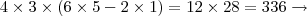
Concluindo, 4\times3\times(6\times5-2\times1)=12\times28=336 \rightarrow alternativa c.
alexandre32100
 
Voltar ao topo

Re: Análise combinatória (P.F.C)

Mensagempor DanielRJ » Ter Ago 24, 2010 15:42

Obrigado alexandre cheguei a esboçar isso mas pensei errado valeu!
Avatar do usuário
DanielRJ
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 254
Registrado em: Sex Ago 20, 2010 18:19
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo
Responder

Voltar para Estatística

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum