 por jmario » Qui Mai 13, 2010 08:41
por jmario » Qui Mai 13, 2010 08:41
Eu tenho a seguinte restrição orçamentária
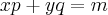
Logo:
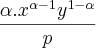
=
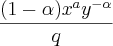
Dessa igualdade, eu tenho esse resultado e não sei como se chegou nele
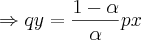
Grato
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por MarceloFantini » Qui Mai 13, 2010 20:50
por MarceloFantini » Qui Mai 13, 2010 20:50
Não sei o que essa equação significa, mas como chegar no resultado é simples. Multiplicando os dois lados por
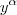
, tem-se:
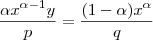
Multiplicando os dois lados por
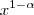
:
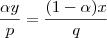
Finalmente, multiplicando os dois lados por
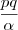
:
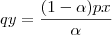
Qualquer dúvida comente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jmario » Sex Mai 14, 2010 09:06
por jmario » Sex Mai 14, 2010 09:06
Muito obrigado.
Eu entendi.
Só gostaria de saber como eu vou escolher o
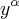
e depois o
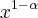
e finalmente
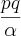
para fazer as multiplicações.
Caso apareça outras equações dessas para resolver, qual o critério que eu uso para multiplicar dos dois lados?
E mais uma vez obrigado
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por MarceloFantini » Sáb Mai 15, 2010 15:47
por MarceloFantini » Sáb Mai 15, 2010 15:47
Se o problema queria que você isolasse o
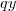
, então é como se você jogasse tudo de y pra um lado e tudo de x pro outro e trabalhasse com as potências (foi o que eu fiz). É que "jogar pra um lado" é na verdade multiplicar os dois por uma mesma coisa.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jmario » Seg Mai 17, 2010 08:44
por jmario » Seg Mai 17, 2010 08:44
E agora eu tenho esse novo isolamento que eu não sei como fazer
![\lambda=\frac{\alpha\left(\frac{\alpha.m}{p} \right)^{\alpha-1}\left[\left(1-\alpha \right).\frac{m}{q} \right]^{1-\alpha}}{p} \lambda=\frac{\alpha\left(\frac{\alpha.m}{p} \right)^{\alpha-1}\left[\left(1-\alpha \right).\frac{m}{q} \right]^{1-\alpha}}{p}](/latexrender/pictures/43738210c050a8c058b6965267989cec.png)
Como eu faço para chegar nesse resultado
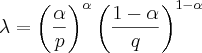
Me ajude mais uma vez.
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por MarceloFantini » Seg Mai 17, 2010 18:49
por MarceloFantini » Seg Mai 17, 2010 18:49
José Mario, por favor crie um novo tópico para essa nova questão, assim evitamos amontoar várias dúvidas em um mesmo lugar, facilitado a localização de todas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jmario » Ter Mai 18, 2010 18:12
por jmario » Ter Mai 18, 2010 18:12
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por MarceloFantini » Ter Mai 18, 2010 19:33
por MarceloFantini » Ter Mai 18, 2010 19:33
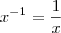
. Se você dividir alguma coisa (um y qualquer, por exemplo) por

dá:
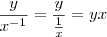
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função lagrangeana
por jmario » Sex Mai 21, 2010 09:23
- 0 Respostas
- 1313 Exibições
- Última mensagem por jmario

Sex Mai 21, 2010 09:23
Funções
-
- isolamento de função
por jmario » Ter Mai 18, 2010 09:13
- 1 Respostas
- 1251 Exibições
- Última mensagem por MarceloFantini

Ter Mai 18, 2010 19:59
Funções
-
- lagrangeana
por jmario » Ter Mai 11, 2010 17:32
- 0 Respostas
- 913 Exibições
- Última mensagem por jmario

Ter Mai 11, 2010 17:32
Sistemas de Equações
-
- isolamento de equação
por jmario » Seg Mai 10, 2010 12:39
- 6 Respostas
- 3059 Exibições
- Última mensagem por jmario

Ter Mai 11, 2010 16:03
Funções
-
- isolamento de variável
por jmario » Sex Jun 04, 2010 08:39
- 3 Respostas
- 3701 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 13:02
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
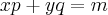
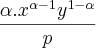 =
= 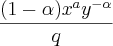
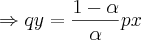

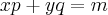
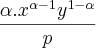 =
= 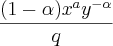
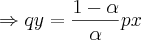

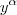 , tem-se:
, tem-se: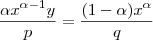
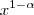 :
: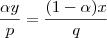
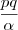 :
: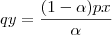


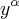 e depois o
e depois o 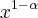 e finalmente
e finalmente 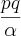 para fazer as multiplicações.
para fazer as multiplicações.
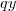 , então é como se você jogasse tudo de y pra um lado e tudo de x pro outro e trabalhasse com as potências (foi o que eu fiz). É que "jogar pra um lado" é na verdade multiplicar os dois por uma mesma coisa.
, então é como se você jogasse tudo de y pra um lado e tudo de x pro outro e trabalhasse com as potências (foi o que eu fiz). É que "jogar pra um lado" é na verdade multiplicar os dois por uma mesma coisa.

![\lambda=\frac{\alpha\left(\frac{\alpha.m}{p} \right)^{\alpha-1}\left[\left(1-\alpha \right).\frac{m}{q} \right]^{1-\alpha}}{p} \lambda=\frac{\alpha\left(\frac{\alpha.m}{p} \right)^{\alpha-1}\left[\left(1-\alpha \right).\frac{m}{q} \right]^{1-\alpha}}{p}](/latexrender/pictures/43738210c050a8c058b6965267989cec.png)
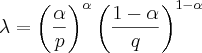




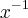 passa para o outro lado só como
passa para o outro lado só como  e perde o
e perde o 


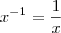 . Se você dividir alguma coisa (um y qualquer, por exemplo) por
. Se você dividir alguma coisa (um y qualquer, por exemplo) por  dá:
dá: 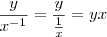 .
.


 .
.
 :
: