- Mostre que
![[f(x)^g(x)]' = f(x)^g(x).[g(x)ln(f(x))]' [f(x)^g(x)]' = f(x)^g(x).[g(x)ln(f(x))]'](/latexrender/pictures/3e343f76b7b8bc43d118469ce31fbf78.png) ((ali é f(x)^g(x) , o x fica embaixo...=/))
((ali é f(x)^g(x) , o x fica embaixo...=/))- Utilizando o resultado acima determine
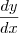 , onde y =
, onde y = 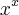
Não to conseguindo chegar a resposta certa nessa 2 questão, =/

![[f(x)^g(x)]' = f(x)^g(x).[g(x)ln(f(x))]' [f(x)^g(x)]' = f(x)^g(x).[g(x)ln(f(x))]'](/latexrender/pictures/3e343f76b7b8bc43d118469ce31fbf78.png) ((ali é f(x)^g(x) , o x fica embaixo...=/))
((ali é f(x)^g(x) , o x fica embaixo...=/))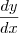 , onde y =
, onde y = 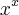




![u=\sqrt[]{x} u=\sqrt[]{x}](/latexrender/pictures/8d064050f5c0ff1b6a1f2ef8358a672a.png)
![{[sen(\sqrt[]{x})]}^{\prime}={(\sqrt[]{x})}^{\prime}.cos(\sqrt[]{x}) {[sen(\sqrt[]{x})]}^{\prime}={(\sqrt[]{x})}^{\prime}.cos(\sqrt[]{x})](/latexrender/pictures/ffdecc7d5c30598c6a9b738e329e0e9f.png)
![{[sen(\sqrt[]{x})]}^{\prime}=\frac{1}{2.\sqrt[]{x}}.cos(\sqrt[]{x}) {[sen(\sqrt[]{x})]}^{\prime}=\frac{1}{2.\sqrt[]{x}}.cos(\sqrt[]{x})](/latexrender/pictures/1a8129a39bac21af6f425bb0101da7e6.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: