 por zenildo » Ter Jul 30, 2013 19:56
por zenildo » Ter Jul 30, 2013 19:56
Numa olimpíada, foram colocadas, numa pista retilínea, 30 tochas acesas, distando 3 metros uma da outra e um recipiente contendo água a 1 metro antes da primeira tocha. Um corredor deveria partir do local onde está o recipiente, pegar a primeira tocha, retornar ao poto de partida para apagá-la e repetir esse movimento até apagar a 30 tocha. Sabendo-se que x expressa a quantidade total de metros percorridos, determine a soma dos algarismos que compõem o n° x.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Russman » Qua Jul 31, 2013 01:23
por Russman » Qua Jul 31, 2013 01:23
Questão interessante. Trata-se da soma de valores que seguem uma P.A. e , embora simples, devemos resolvê-la atentamente.
Vamos colocar a tocha de número

no metro 0. Isto é, se
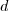
indica a quantidade de metros medidos, então
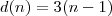
. Nesta configuração, a tocha encontra-se em

.
Correndo de uma posição
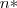
qualquer até a tocha (partindo do metro -1) o corredor terá percorrido a distância
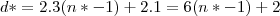
pois ele está em

, passa por
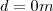
, corre até
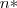
, volta para

e então retorna a tocha em

.
Deste modo a distância total

percorrida pelo corredor será dada por
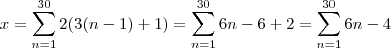
Agora podemos simplificar a soma para
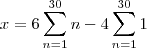
e lembrando que
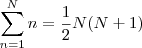
e
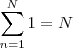
então
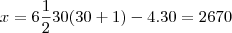
.
Portanto, a soma dos algarismo deve ser
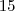
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por zenildo » Dom Set 01, 2013 15:28
por zenildo » Dom Set 01, 2013 15:28
eu queria saber se haveria a possibilidade desse calculo ser mais de raciocinio logico do que aplicar formulas.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por zenildo » Dom Set 01, 2013 17:20
por zenildo » Dom Set 01, 2013 17:20
Esse problema pederia ter sido resolvido através do raciocínio lógico?
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Russman » Seg Set 02, 2013 10:44
por Russman » Seg Set 02, 2013 10:44
A única fórmula que eu apliquei foi a da soma de 1 a N. O desenvolvimento da distância percorrida com relação a posição da tocha foi justamente lógica.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por zenildo » Seg Set 02, 2013 16:30
por zenildo » Seg Set 02, 2013 16:30
Eu não quero dizer que seu problema está ilógico, eu me referia mais o modo de fazê-lo, pois em uma escola técnica, eles tendem a simplificá-lo de forma a reduzir tempo.Como assim? Porque as questões do Enem em média , leva 2 minutos a 3 minutos cada, logo o tempo é ouro.Mas valeu, todo a ajuda é bem vinda à formação do conhecimento, agradecido.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 no metro 0. Isto é, se
no metro 0. Isto é, se 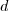 indica a quantidade de metros medidos, então
indica a quantidade de metros medidos, então 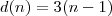 . Nesta configuração, a tocha encontra-se em
. Nesta configuração, a tocha encontra-se em  .
. 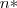 qualquer até a tocha (partindo do metro -1) o corredor terá percorrido a distância
qualquer até a tocha (partindo do metro -1) o corredor terá percorrido a distância 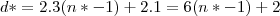
 , passa por
, passa por 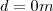 , corre até
, corre até 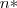 , volta para
, volta para  e então retorna a tocha em
e então retorna a tocha em  .
. percorrida pelo corredor será dada por
percorrida pelo corredor será dada por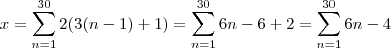
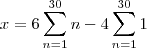
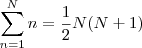
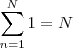
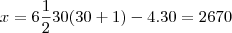 .
.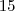






 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.