 por Jaqueline Pimenta » Qui Out 01, 2009 11:50
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
Bom dia,

Estou com dificuldades em um exercicio de fatoração, que por várias tentativas não consegui desenvolver! Ajudem-me, por favor!
Ex: Se x e y são números reais tais que x.y

0 e |x|

|y|, a expressão
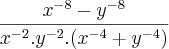
é equivalente a:
Tentativas:
1° - Fatorar o numerador

como Diferença de quadrados, tranformando primeiro, o indice -8 em -4.2 resultando em
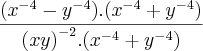
. Em seguida cortei no numerador e no denominador a expressão

, que resultou em
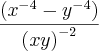
. E a partir dai, não sei o que fazer, por ser uma subtração sobre uma multiplicação. E mesmo que eu faça outra fatoração como diferença de quadrados no numerador que ainda é possível, não sairia disso!

2°- Desenvolver a multiplicação no denominador, para conseguir um fator comum ou até mesmo cancelar com o numerador. Mas não houve sucesso algum.

Dúvida: Gostaria de saber o que as informações x.y

0 e |x|

|y|, aprensentadas no enunciado do exercicio, me acrescentam.
Desde já agradeço e parabenizo o site, acredito que será de boa importancia para os estudos.

Jaque Pimenta
-
Jaqueline Pimenta
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Set 30, 2009 11:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando
- Andamento: formado
 por Elcioschin » Qui Out 01, 2009 17:59
por Elcioschin » Qui Out 01, 2009 17:59
Pimenta
Você tem a resposta ou as alternativas?
Sugestão para continuar
No numerador ----> x^-4 - y^-4 = (x^-2 + y^-2)*(x^-2 - y^-2) = (x^-2 + y^-2)*(1/x² - 1/y²) = (x^-2 + y^-2)*(y² - x²)/x²y²
No denominador ----> 1/x²y²
Ao dividir desaparece 1/x²y² e sobra ----> (x^-2 + y^-2)*(y² - x²) = (1/x² + 1/y²)*(y + x)*(y - x) = (y² + x²)*(y + x)*(y - x)*x²y²
Como você não postou a solução nem as alternativas, não sei se esta é a resposta final.
Quanto às tuas dúvidas sobre x, y diferentes de zero e |x! diferente de |y|:
Se x= o ou y = 0 ou x = - y ----> anula o denominador, o que não é permitido (divisão por zero).
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Jaqueline Pimenta » Qui Out 01, 2009 21:40
por Jaqueline Pimenta » Qui Out 01, 2009 21:40
Oi Elcioschin

Agradeço por responder!
Já tinha chegado a está resolução, mas não é a resposta.

De acordo com o livro seria
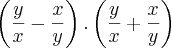
ou sem fatorar
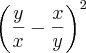
Eita, que adoro matemática. Mas este exercicio está me encabulando kkkk
Pretendo fazer Engenharia tbm!

-
Jaqueline Pimenta
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Set 30, 2009 11:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando
- Andamento: formado
 por Elcioschin » Dom Out 04, 2009 21:02
por Elcioschin » Dom Out 04, 2009 21:02
Jaqueline
Vamos fazer desde o início, transformando os expoentes negativos em positivos, para facilitar:
V = (x^-8 - y^-8)/[(x*y)^-2](x^-4 + y^-4) -----> V = (1/x^8 - 1/y^8)/(1/x²*y²)*(1/x^4 + 1/y^4)
V = [(y^8 - x^8)/(x^8*y^8)]/(1/x²*y²)*[(y^4 + x^4)/^(y^4*x^4)]
Simplificando x^8*y^8 com x²*y² e com x^4*y^4 sobra:
V = (y^8 - x^8)/(x²*y²)*(y^4 + x^4) -----> Fatorando (y^8 - x^8):
V = (y^4 + x^4)*(y^4 - x^4)/(x²y²)*(y^4 + x^4) -----> V = (y^4 - x^4)/x²*y² ----> Expressão equivalente a sua, com expoentes positivos
V = y^4/x²*y² - x^4/x²*y² -----> V = y²/x² - x²/y² -----> Fatorando ----> V = (y/x - x/y)*(y/x + x/y) ----> Resposta do livro
Não concordo, contudo, com a última expressão da resposta " ou sem fatorar (y/x - x/y)² "
Este resultado NÃO é igual à primeira resposta correta do livro ----> (y/x - x/y)² = y²/x² + x²/y² - 2 ----> Compare com a resposta certa!!!!
Para estar certa deveria ser (y/x)² - (x/y)² = y²/x² - x²/y² = (y/x - x/y)*(y/x + x/y)
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Jaqueline Pimenta » Seg Out 05, 2009 12:05
por Jaqueline Pimenta » Seg Out 05, 2009 12:05
Oi Elcioschin!
Agradeço pela resolução!!!

Finalmente aprendi!!!
Depois de um ano sem estudar, perdi o jeito da coisa!! kk
As regras gerais sei de cor!
Porém não desenvolvo e complico com o mais básico; Adição, subtração, multiplicação e divisão, sinais e pequenos detalhes como o erro na ultima resposta que enviei.

Se tiver mais dicas, serão de bom agrado!!!
Grata,
Jaqueline
-
Jaqueline Pimenta
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Set 30, 2009 11:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8921 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3262 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8829 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2545 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- fatoração
por jose henrique » Ter Out 26, 2010 23:17
- 2 Respostas
- 1386 Exibições
- Última mensagem por jose henrique

Qua Out 27, 2010 07:29
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 0 e |x|
0 e |x|  |y|, a expressão
|y|, a expressão 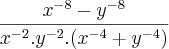 é equivalente a:
é equivalente a: como Diferença de quadrados, tranformando primeiro, o indice -8 em -4.2 resultando em
como Diferença de quadrados, tranformando primeiro, o indice -8 em -4.2 resultando em 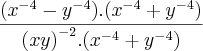 . Em seguida cortei no numerador e no denominador a expressão
. Em seguida cortei no numerador e no denominador a expressão  , que resultou em
, que resultou em 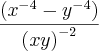 . E a partir dai, não sei o que fazer, por ser uma subtração sobre uma multiplicação. E mesmo que eu faça outra fatoração como diferença de quadrados no numerador que ainda é possível, não sairia disso!
. E a partir dai, não sei o que fazer, por ser uma subtração sobre uma multiplicação. E mesmo que eu faça outra fatoração como diferença de quadrados no numerador que ainda é possível, não sairia disso! 
 0 e |x|
0 e |x|  |y|, aprensentadas no enunciado do exercicio, me acrescentam.
|y|, aprensentadas no enunciado do exercicio, me acrescentam.


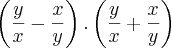 ou sem fatorar
ou sem fatorar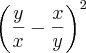





 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.