
Estou com dificuldades em um exercicio de fatoração, que por várias tentativas não consegui desenvolver! Ajudem-me, por favor!
Ex: Se x e y são números reais tais que x.y
 0 e |x|
0 e |x|  |y|, a expressão
|y|, a expressão 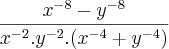 é equivalente a:
é equivalente a:Tentativas:
1° - Fatorar o numerador
 como Diferença de quadrados, tranformando primeiro, o indice -8 em -4.2 resultando em
como Diferença de quadrados, tranformando primeiro, o indice -8 em -4.2 resultando em 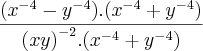 . Em seguida cortei no numerador e no denominador a expressão
. Em seguida cortei no numerador e no denominador a expressão  , que resultou em
, que resultou em 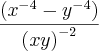 . E a partir dai, não sei o que fazer, por ser uma subtração sobre uma multiplicação. E mesmo que eu faça outra fatoração como diferença de quadrados no numerador que ainda é possível, não sairia disso!
. E a partir dai, não sei o que fazer, por ser uma subtração sobre uma multiplicação. E mesmo que eu faça outra fatoração como diferença de quadrados no numerador que ainda é possível, não sairia disso! 
2°- Desenvolver a multiplicação no denominador, para conseguir um fator comum ou até mesmo cancelar com o numerador. Mas não houve sucesso algum.
Dúvida: Gostaria de saber o que as informações x.y
 0 e |x|
0 e |x|  |y|, aprensentadas no enunciado do exercicio, me acrescentam.
|y|, aprensentadas no enunciado do exercicio, me acrescentam.Desde já agradeço e parabenizo o site, acredito que será de boa importancia para os estudos.
Jaque Pimenta



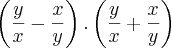 ou sem fatorar
ou sem fatorar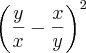



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.