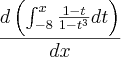
Entretanto estou com duvida na hora de achar a primitiva.
eu não consigo fazer uma substituição valida mesmo quebrando ela em duas..
Como vou integrar e depois derivar, então vou chegar no mesmo resultdo, então o resultado seria:
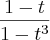
e eu avaliaria nos pontos -8 e x
Mas ai eu teria que primeiro passar pelo x não é?
Como será essa resolução? esse tipo de exercício tem haver com algum teorema ou alguma técnica de integração??
obrigado


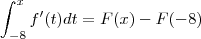 .
. 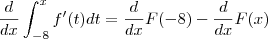 .
. 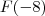 nos fornecerá um número real sua derivada é nula .Logo,
nos fornecerá um número real sua derivada é nula .Logo, 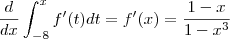 ou
ou 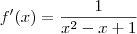

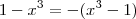 por
por  . Assim ,
. Assim , ![- (x^3 - 1) = -(x-1)[x^2 + x + 1 ] = (1-x)[x^2 + x + 1 ] - (x^3 - 1) = -(x-1)[x^2 + x + 1 ] = (1-x)[x^2 + x + 1 ]](/latexrender/pictures/3f26bcd23ce56a292822a95c852c7e76.png) .
. .
. 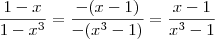 .
. 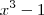 por
por  vamos obter que
vamos obter que 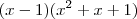 .Logo ,
.Logo , 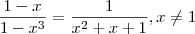
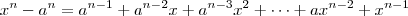 ou de forma compacta
ou de forma compacta 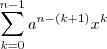 . Basta dividir
. Basta dividir  por
por 
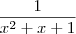

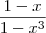 obtendo
obtendo 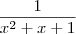 sem deixar claro que
sem deixar claro que  . Caso contrário , por um lado
. Caso contrário , por um lado  .Entretanto, por outro lado
.Entretanto, por outro lado 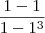 ???? (Não estar definido ) .
???? (Não estar definido ) .  (que não estar definido) . Note que
(que não estar definido) . Note que  estar em vizinhança do número 1 ,por isso é natural que os limites laterais resultam um número bem próximo de 1/3 .(Mas não 1/3 ) .
estar em vizinhança do número 1 ,por isso é natural que os limites laterais resultam um número bem próximo de 1/3 .(Mas não 1/3 ) .  e
e 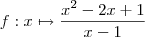 .
. 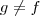 pois
pois 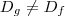 .Pois
.Pois 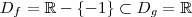 e domínio de
e domínio de  não estar contido no domínio de
não estar contido no domínio de  .
. 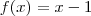
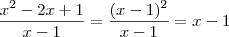 . É bem provável que alguém afirme que
. É bem provável que alguém afirme que  . Mas note que isto não é verdade , só fizermos esta simplificação com o domínio da função
. Mas note que isto não é verdade , só fizermos esta simplificação com o domínio da função 
 .
.



