 por fabriel » Sáb Jan 05, 2013 21:42
por fabriel » Sáb Jan 05, 2013 21:42
Oi pessoal preciso calcular essa integral:
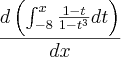
Entretanto estou com duvida na hora de achar a primitiva.
eu não consigo fazer uma substituição valida mesmo quebrando ela em duas..
Como vou integrar e depois derivar, então vou chegar no mesmo resultdo, então o resultado seria:
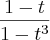
e eu avaliaria nos pontos -8 e x
Mas ai eu teria que primeiro passar pelo x não é?
Como será essa resolução? esse tipo de exercício tem haver com algum teorema ou alguma técnica de integração??
obrigado
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Sáb Jan 05, 2013 23:02
por e8group » Sáb Jan 05, 2013 23:02
Suponhamos que ,
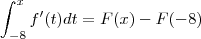
.
Temos então,
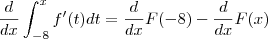
.
Como
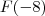
nos fornecerá um número real sua derivada é nula .Logo,
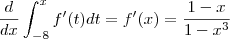
ou
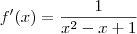
.Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Dom Jan 06, 2013 00:02
por fabriel » Dom Jan 06, 2013 00:02
humm obrigado
Eu só não entendi essa parte:
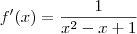
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Dom Jan 06, 2013 00:49
por e8group » Dom Jan 06, 2013 00:49
Boa noite , basta fazer a divisão de
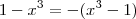
por

. Assim ,
![- (x^3 - 1) = -(x-1)[x^2 + x + 1 ] = (1-x)[x^2 + x + 1 ] - (x^3 - 1) = -(x-1)[x^2 + x + 1 ] = (1-x)[x^2 + x + 1 ]](/latexrender/pictures/3f26bcd23ce56a292822a95c852c7e76.png)
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Dom Jan 06, 2013 12:15
por fabriel » Dom Jan 06, 2013 12:15
hummm entendi então foi um Artificio Algébrico.. Então podemos concluir que a solução é:
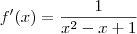
não é mesmo??
obrigado!!
Um abraço!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Dom Jan 06, 2013 12:46
por e8group » Dom Jan 06, 2013 12:46
Não .Peço desculpas , copiei erroneamente a primeira resposta . O correto é

.
Veja por que ,
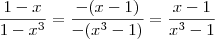
.
Assim fazendo a divisão de
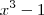
por

vamos obter que
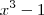
=
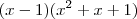
.Logo ,
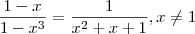
Tem um caso geral
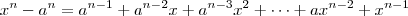
ou de forma compacta
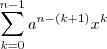
. Basta dividir

por

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Dom Jan 06, 2013 13:30
por fabriel » Dom Jan 06, 2013 13:30
Mas eu tenho que excluir o 1?
Pois Se calcularmos os limites laterais dessa função:
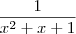
Obteremos:

logo esse limite quando x tende a 1 existe, que é:

Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Dom Jan 06, 2013 14:13
por e8group » Dom Jan 06, 2013 14:13
Boa tarde .Note que em hipótese nenhuma podemos fazer a simplificação
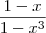
obtendo
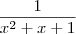
sem deixar claro que

. Caso contrário , por um lado

.Entretanto, por outro lado
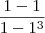
???? (Não estar definido ) .
Acontece que tomar limite quando x tende a 1 .É diferente que calcular

(que não estar definido) . Note que

estar em vizinhança do número 1 ,por isso é natural que os limites laterais resultam um número bem próximo de 1/3 .(Mas não 1/3 ) .
Façamos uma analogia , Sejam

e
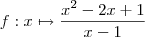
.
Perceba que
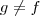
pois
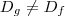
.Pois
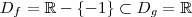
e domínio de

não estar contido no domínio de

.
Mas note que
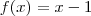
. Pois
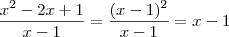
. É bem provável que alguém afirme que

. Mas note que isto não é verdade , só fizermos esta simplificação com o domínio da função

bem definido .
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Dom Jan 06, 2013 14:50
por fabriel » Dom Jan 06, 2013 14:50
Boa tarde. Ok obrigado!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Dúvida com uma integral simples
por Leonardo Ribeiro » Sex Abr 03, 2015 20:02
- 1 Respostas
- 2087 Exibições
- Última mensagem por Leonardo Ribeiro

Sex Abr 03, 2015 21:06
Cálculo: Limites, Derivadas e Integrais
-
- [integral] duvida integral
por lucasdemirand » Ter Nov 26, 2013 17:47
- 0 Respostas
- 906 Exibições
- Última mensagem por lucasdemirand

Ter Nov 26, 2013 17:47
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em Integral
por Cleyson007 » Ter Fev 28, 2012 17:36
- 5 Respostas
- 2197 Exibições
- Última mensagem por LuizAquino

Qui Mar 01, 2012 16:27
Cálculo: Limites, Derivadas e Integrais
-
- Duvida na Integral
por rodrigo ff » Sex Mar 23, 2012 17:44
- 1 Respostas
- 1535 Exibições
- Última mensagem por DanielFerreira

Sex Mar 23, 2012 19:01
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] - Dúvida
por digsydinner » Ter Mar 27, 2012 10:37
- 3 Respostas
- 1867 Exibições
- Última mensagem por LuizAquino

Sex Mar 30, 2012 00:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
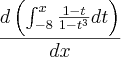
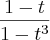


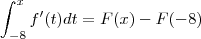 .
. 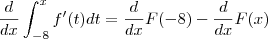 .
. 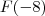 nos fornecerá um número real sua derivada é nula .Logo,
nos fornecerá um número real sua derivada é nula .Logo, 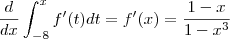 ou
ou 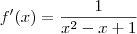

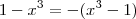 por
por  . Assim ,
. Assim , ![- (x^3 - 1) = -(x-1)[x^2 + x + 1 ] = (1-x)[x^2 + x + 1 ] - (x^3 - 1) = -(x-1)[x^2 + x + 1 ] = (1-x)[x^2 + x + 1 ]](/latexrender/pictures/3f26bcd23ce56a292822a95c852c7e76.png) .
. .
. 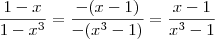 .
. 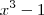 por
por  vamos obter que
vamos obter que 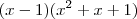 .Logo ,
.Logo , 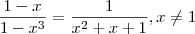
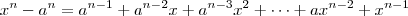 ou de forma compacta
ou de forma compacta 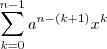 . Basta dividir
. Basta dividir  por
por 
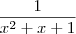

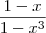 obtendo
obtendo 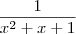 sem deixar claro que
sem deixar claro que  . Caso contrário , por um lado
. Caso contrário , por um lado  .Entretanto, por outro lado
.Entretanto, por outro lado 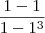 ???? (Não estar definido ) .
???? (Não estar definido ) .  (que não estar definido) . Note que
(que não estar definido) . Note que  estar em vizinhança do número 1 ,por isso é natural que os limites laterais resultam um número bem próximo de 1/3 .(Mas não 1/3 ) .
estar em vizinhança do número 1 ,por isso é natural que os limites laterais resultam um número bem próximo de 1/3 .(Mas não 1/3 ) .  e
e 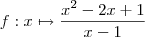 .
. 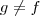 pois
pois 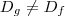 .Pois
.Pois 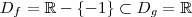 e domínio de
e domínio de  não estar contido no domínio de
não estar contido no domínio de  .
. 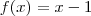
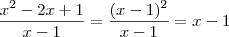 . É bem provável que alguém afirme que
. É bem provável que alguém afirme que  . Mas note que isto não é verdade , só fizermos esta simplificação com o domínio da função
. Mas note que isto não é verdade , só fizermos esta simplificação com o domínio da função