 por Claudin » Seg Jul 09, 2012 19:46
por Claudin » Seg Jul 09, 2012 19:46
Determine a equação cartesiana do plano
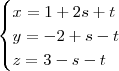
Não sei como transformar para forma cartesiana, seria uma passagem de paramétricas para equação cartesiana?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por DanielFerreira » Sáb Jul 14, 2012 00:32
por DanielFerreira » Sáb Jul 14, 2012 00:32
Olá Claudin,
boa noite!
Inicialmente, devemos encontrar um vetor
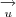
perpendicular ao plano;
Consideremos suas coordenadas...
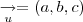
;
Com isso:
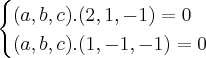
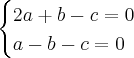
Teremos:
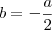
e
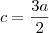
Considerando

,
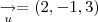
Sabendo que a equação cartesiana é dada por

, então,

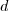
é obtido substituindo o ponto do plano
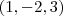
na equação, portanto,...

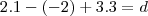

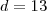
Daí,

Espero ter ajudado!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Sáb Jul 14, 2012 01:13
por MarceloFantini » Sáb Jul 14, 2012 01:13
É interessante notar outra forma de resolver este problema, tomando o produto vetorial dos vetores diretores do plano para encontrar o vetor normal:
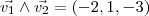
,
de onde

e como o ponto

pertence ao plano, temos
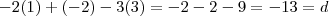
,
portanto

, ou multiplicando por menos um para trocar o sinal,

.
Note que o vetor normal encontrado pelo produto vetorial foi um múltiplo do vetor encontrado pelo Danjr, como deveria ser.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Russman » Sáb Jul 14, 2012 02:29
por Russman » Sáb Jul 14, 2012 02:29
Só para completar a excelente abordagem do Moderador ao problema, eu gostaria de expor a solução do problema de forma a expressar o plano como solução uma equação vetorial!
Veja que, se
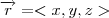
é o raio-vetor do espaço
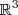
, então, se

,
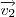
e
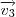
são vetores constantes, a equação vetorial do plano é dada por
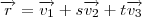
,
onde

e

são parâmetros.
Concordando que um vetor
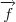
, de forma que
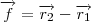
,
isto é, seja obtido da subtração de dois raio-vetores quaisquer dessa superfície seja paralelo/pertencente ao plano, então, com isso, podemos provar que os vetores
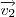
e
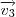
são a base de qualquer outro vetor pertencente a esse plano! Veja,
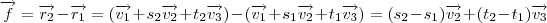
.
Vemos que o vetor
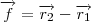
é combinação linear dos vetores acima. Logo estes são base para o espaço entendido pelo plano e , portanto, seus chamados vetores diretores!
Assim, um vetor
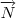
que seja normal ao plano é obtido tomando
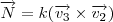
,
isto é, tomando o produto vetorial dos vetores diretores!
Ainda, você pode provar esse fato, como exercício, tomando 3 vetores
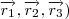
e obtendo o vetor normal
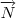
da seguinte forma
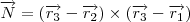
.
Desenvolvendo este produto você chegará a mesma conclusão.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Seg Jul 16, 2012 03:20
por Claudin » Seg Jul 16, 2012 03:20
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por DanielFerreira » Seg Jul 16, 2012 20:55
por DanielFerreira » Seg Jul 16, 2012 20:55
Vlw.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Claudin » Seg Jul 16, 2012 22:48
por Claudin » Seg Jul 16, 2012 22:48
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5269 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14857 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2704 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Plano
por Rhyu » Dom Abr 08, 2012 10:57
- 2 Respostas
- 1915 Exibições
- Última mensagem por MarceloFantini

Seg Abr 09, 2012 03:40
Geometria Analítica
-
- Plano
por Claudin » Sex Jul 06, 2012 12:32
- 2 Respostas
- 1748 Exibições
- Última mensagem por Claudin

Sex Jul 06, 2012 16:23
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
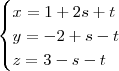

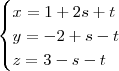

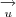 perpendicular ao plano;
perpendicular ao plano;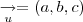 ;
;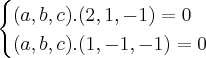
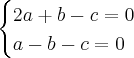
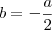 e
e 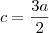
 ,
, 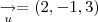
 , então,
, então, 
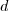 é obtido substituindo o ponto do plano
é obtido substituindo o ponto do plano 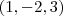 na equação, portanto,...
na equação, portanto,...
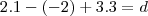

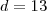


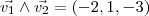 ,
,
 pertence ao plano, temos
pertence ao plano, temos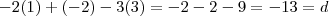 ,
, , ou multiplicando por menos um para trocar o sinal,
, ou multiplicando por menos um para trocar o sinal,  .
.

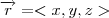 é o raio-vetor do espaço
é o raio-vetor do espaço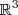 , então, se
, então, se  ,
, 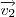 e
e 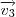 são vetores constantes, a equação vetorial do plano é dada por
são vetores constantes, a equação vetorial do plano é dada por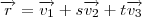 ,
, e
e  são parâmetros.
são parâmetros.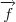 , de forma que
, de forma que 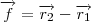 ,
,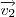 e
e 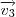 são a base de qualquer outro vetor pertencente a esse plano! Veja,
são a base de qualquer outro vetor pertencente a esse plano! Veja,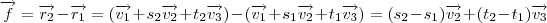 .
.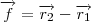 é combinação linear dos vetores acima. Logo estes são base para o espaço entendido pelo plano e , portanto, seus chamados vetores diretores!
é combinação linear dos vetores acima. Logo estes são base para o espaço entendido pelo plano e , portanto, seus chamados vetores diretores!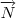 que seja normal ao plano é obtido tomando
que seja normal ao plano é obtido tomando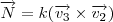 ,
,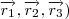 e obtendo o vetor normal
e obtendo o vetor normal 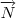 da seguinte forma
da seguinte forma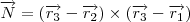 .
.








