 por karen » Sáb Mai 12, 2012 17:15
por karen » Sáb Mai 12, 2012 17:15
Eu sei que sen(a+b) = senacosb + senbcosa, mas não consigo aplicar a fórmula na seguinte situação:
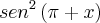
O exercício pede que eu resolve a seguinte equação:
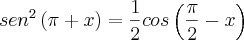
Já resolvi a segunda parte da equação que deu senx
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
 por DanielFerreira » Sáb Mai 12, 2012 20:48
por DanielFerreira » Sáb Mai 12, 2012 20:48
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Sáb Mai 12, 2012 21:54
por DanielFerreira » Sáb Mai 12, 2012 21:54
Karen,
resolvi a segunda parte e achei
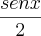
, talvez tenha esquecido multiplicar por

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por karen » Ter Mai 15, 2012 18:42
por karen » Ter Mai 15, 2012 18:42
Entendi sim, muito boa explicação obrigada!
Pois é, esqueci de multiplicar por 1/2.
Obrigada
-
karen
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Mai 03, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Eletrônica
- Andamento: formado
 por DanielFerreira » Sáb Mai 19, 2012 10:19
por DanielFerreira » Sáb Mai 19, 2012 10:19
Não há de quê.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
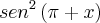
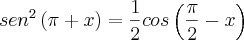

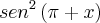
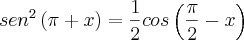

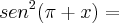
![[sen(\pi + x)]^2 = [sen(\pi + x)]^2 =](/latexrender/pictures/5c3c24f4ec05466c4894f98ebc367960.png)
![[sen\pi . cos x + senx . cos\pi]^2 = [sen\pi . cos x + senx . cos\pi]^2 =](/latexrender/pictures/1e5896d98f8dd8189c652872766ba457.png)
![[0 . cos x + senx . - 1]^2 = [0 . cos x + senx . - 1]^2 =](/latexrender/pictures/88ebd53476d78ce6a6c80dfc52b521ab.png)
![[0 - senx]^2 = [0 - senx]^2 =](/latexrender/pictures/3834b359f3ae772b38ef0c4bd2ef65de.png)
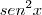

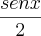 , talvez tenha esquecido multiplicar por
, talvez tenha esquecido multiplicar por 




 .
.
 :
: