 por beel » Dom Nov 20, 2011 22:12
por beel » Dom Nov 20, 2011 22:12
Nessa integral
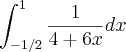
qual seria o "u" pra fazer a substituiçao?pra mim so poderia ser 4 + 6x
mas assim o "du" seria: 6dx...
fazendo assim, meu resultado deu
ln|6.10| - ln |6.1|
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Dom Nov 20, 2011 23:03
por MarceloFantini » Dom Nov 20, 2011 23:03
Porque não avaliar direto?
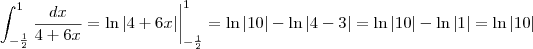
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por beel » Ter Nov 22, 2011 13:52
por beel » Ter Nov 22, 2011 13:52
vi onde errei, mas meu resultado deu ln |10| / 6
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Ter Nov 22, 2011 19:10
por MarceloFantini » Ter Nov 22, 2011 19:10
Realmente, falta um pedaço. Vamos fazer passo a passo: faça
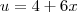
, daí
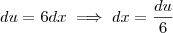
, logo
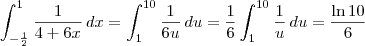
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] integral - substituiçao trigonometrica
por beel » Dom Nov 27, 2011 17:30
- 1 Respostas
- 1810 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:19
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral por substituiçao trigonometrica 2
por beel » Dom Nov 27, 2011 18:06
- 1 Respostas
- 1557 Exibições
- Última mensagem por LuizAquino

Ter Nov 29, 2011 15:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição / Integral por partes
por Carlos28 » Seg Out 19, 2015 12:25
- 1 Respostas
- 3043 Exibições
- Última mensagem por nakagumahissao

Seg Out 19, 2015 23:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição
por Aliocha Karamazov » Qui Fev 23, 2012 23:57
- 2 Respostas
- 2465 Exibições
- Última mensagem por MarceloFantini

Sex Fev 24, 2012 12:07
Cálculo: Limites, Derivadas e Integrais
-
- Integral (substituição)
por kika_sanches » Sex Mar 23, 2012 14:42
- 4 Respostas
- 3138 Exibições
- Última mensagem por kika_sanches

Sex Mar 23, 2012 15:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
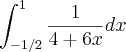

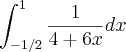



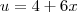 , daí
, daí 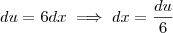 , logo
, logo 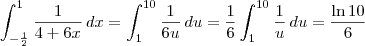 .
.


 .
.
 :
: