 por ewald » Seg Mai 23, 2011 13:09
por ewald » Seg Mai 23, 2011 13:09
Oi to estudando por esse livro e nao consegui fazer os exercicios propostos da primeira parte de 14 pra cima. Eu devo ter perdido algo. Acredito que se me ajudarem com o exercicio abaixo eu consigo deduzir a forma de fazer os outros.
" Os lados de um triangulo retangulo ABC (reto em A) medem 5, 12, 13. Calcular AB . AC + BA . BC + CA . CB." - Uma das minhas duvidas por exemplo é se as medidas que ele fornece sao distancias entre pontos ou o modulo do vetor (lado do triangulo).
Obs.: nao consegui botar o simbolo de vetor mas Ab, AC, BA ... sao vetores.
Obrigado.
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por LuizAquino » Seg Mai 23, 2011 16:51
por LuizAquino » Seg Mai 23, 2011 16:51
DicaComo nada foi informado sobre a posição dos vértices A, B e C do triângulo, vamos representá-lo em um sistema de eixos conveniente, como ilustra a figura abaixo.

- triangulo-ABC.png (2.03 KiB) Exibido 6651 vezes
Note, por exemplo, que nesse sistema temos que
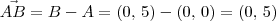
.
ObservaçãoPara inserir o símbolo de vetor, use o comando tex:
- Código: Selecionar todos
[tex]\vec{AB}[/tex]
Isso irá produzir:
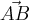
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ewald » Seg Mai 23, 2011 20:13
por ewald » Seg Mai 23, 2011 20:13
Ta mas eu realmente continuo com duvida ... Estou faendo a questao de modo que os lados do triangulo sejam os Vetores que ele pede, ou seja, minha conta ta ficando assim:
(13 . 12) + (13 . 5) + (12 . 5) = 281
No entanto a resposta do livro diz que é 169.
Postei um desenho no imageshack do triangulo que eu fiz (link abaixo).
http://imageshack.us/photo/my-images/718/triv.png/
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por LuizAquino » Seg Mai 23, 2011 22:00
por LuizAquino » Seg Mai 23, 2011 22:00
Você não está sabendo aplicar o produto interno (também chamado de produto escalar).
Dado o vetor
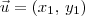
e o vetor
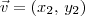
definimos o produto interno entre esses vetores (representado por

) como sendo:
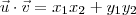
Por exemplo, o produto interno entre
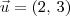
e
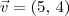
é:
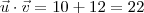
Desse modo, o que você precisa fazer no exercício é determinar cada um dos vetores (como eu fiz para
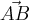
na dica anterior) e em seguida calcular a soma dos produtos internos indicados.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Radiciação] livro 2 do Iezzi- exercicio
por edilviana » Qui Fev 16, 2012 11:39
- 1 Respostas
- 1776 Exibições
- Última mensagem por edilviana

Qui Fev 16, 2012 12:35
Álgebra Elementar
-
- [integrais duplas] Exercício livro diomara
 por gustavoluiss » Qui Jan 16, 2014 22:37
por gustavoluiss » Qui Jan 16, 2014 22:37
- 2 Respostas
- 2422 Exibições
- Última mensagem por Guilherme Pimentel

Sex Jan 17, 2014 03:01
Cálculo: Limites, Derivadas e Integrais
-
- livro de matemática
por DanielFerreira » Sex Mar 26, 2010 12:54
- 1 Respostas
- 3372 Exibições
- Última mensagem por Cleyson007

Sex Mar 26, 2010 17:23
Piadas
-
- PA Livro de Dante
por Joana Gabriela » Seg Ago 09, 2010 10:37
- 1 Respostas
- 3139 Exibições
- Última mensagem por Cleyson007

Seg Ago 09, 2010 14:40
Progressões
-
- Livro de Aritmética
por Abelardo » Qui Mar 31, 2011 17:28
- 1 Respostas
- 2474 Exibições
- Última mensagem por Neperiano

Sex Out 28, 2011 15:38
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


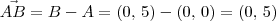 .
.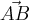

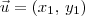 e o vetor
e o vetor 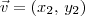 definimos o produto interno entre esses vetores (representado por
definimos o produto interno entre esses vetores (representado por  ) como sendo:
) como sendo: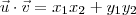
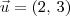 e
e 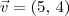 é:
é: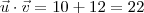
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.