Alguem me ajude no seguinte exercício.
Quando tento fazer e não consigo sonho a noite toda com o exercício.
[b][size=150]2) Sejam dadas duas circunferencias concentricas(mesmocentro) e considere uma corda de comprimento c, da circunferencia exterior, que tangencia a circunferencia interior. Mostre que a area da região comprendida entre as duas circunferencias é igual a pi.{c}^{2}/4.
Lembre que uma reta tangente á uma circunferencia é perpendicular ao raio no ponto de tangencia.
Obrigada!!!!!


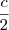 ,
,  e hipotenusa
e hipotenusa 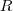 . Sabemos que a área da coroa circular é a área da maior menos a área da menor, ou seja,
. Sabemos que a área da coroa circular é a área da maior menos a área da menor, ou seja, 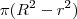 . Aplicando pitágoras no triângulo encontrado:
. Aplicando pitágoras no triângulo encontrado:
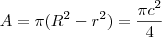



 .
.
 :
: