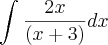
Tentei resolver por substituição. Sei que posso resolver somando e diminuindo três no numerador para separar o denominador e ficar com
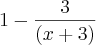 .
.Mas resolvendo por substituição:
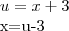
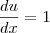

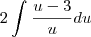
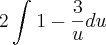
![2\left[u-3Lnu \right]+C 2\left[u-3Lnu \right]+C](/latexrender/pictures/7535c851fb47a911fb048a5531036424.png)
Logo:
![2\left[\left(x+3 \right)-3Ln(x+3) \right]+C 2\left[\left(x+3 \right)-3Ln(x+3) \right]+C](/latexrender/pictures/7eb83629bc1824211cb832907bd1812e.png)
Mas a resposta é:
![2\left[x-3Ln\left(x+3 \right) \right]+c 2\left[x-3Ln\left(x+3 \right) \right]+c](/latexrender/pictures/40404a14eddf59cd1b7bd05341d6fd16.png)
Onde está meu erro?

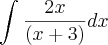
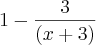 .
.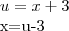
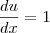

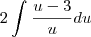
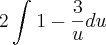
![2\left[u-3Lnu \right]+C 2\left[u-3Lnu \right]+C](/latexrender/pictures/7535c851fb47a911fb048a5531036424.png)
![2\left[\left(x+3 \right)-3Ln(x+3) \right]+C 2\left[\left(x+3 \right)-3Ln(x+3) \right]+C](/latexrender/pictures/7eb83629bc1824211cb832907bd1812e.png)
![2\left[x-3Ln\left(x+3 \right) \right]+c 2\left[x-3Ln\left(x+3 \right) \right]+c](/latexrender/pictures/40404a14eddf59cd1b7bd05341d6fd16.png)

 que surge no processo de integração é arbitrária. Isto é, pode ser qualquer uma. Assim, quando você efetua a multiplicação
que surge no processo de integração é arbitrária. Isto é, pode ser qualquer uma. Assim, quando você efetua a multiplicação 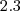 na sua resposta obtém o restante da função somado a um valor constante
na sua resposta obtém o restante da função somado a um valor constante  que é absorvido pela própria constante
que é absorvido pela própria constante  . Veja que isso só se pode fazer quando a constante for arbitrária.
. Veja que isso só se pode fazer quando a constante for arbitrária.

 é tão arbitrário quanto
é tão arbitrário quanto  .
.

![\frac{dy}{dx}=x\sqrt[]{y} \frac{dy}{dx}=x\sqrt[]{y}](/latexrender/pictures/77c5c8f47c4f749b0de05940df6daf64.png)
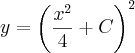
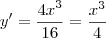
![\frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}} \frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}}](/latexrender/pictures/17a24a5b37c86eb319a075a6a2a6e74a.png)
![\frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}+9} \frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}+9}](/latexrender/pictures/d5de18b9b99c1046ae7590c012fef8ad.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.
 :
: