 por Sobreira » Ter Ago 20, 2013 08:56
por Sobreira » Ter Ago 20, 2013 08:56
Tenho que resolver a seguinte integral:
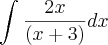
Tentei resolver por substituição. Sei que posso resolver somando e diminuindo três no numerador para separar o denominador e ficar com
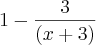
.
Mas resolvendo por substituição:
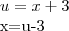
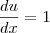

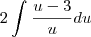
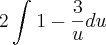
![2\left[u-3Lnu \right]+C 2\left[u-3Lnu \right]+C](/latexrender/pictures/7535c851fb47a911fb048a5531036424.png)
Logo:
![2\left[\left(x+3 \right)-3Ln(x+3) \right]+C 2\left[\left(x+3 \right)-3Ln(x+3) \right]+C](/latexrender/pictures/7eb83629bc1824211cb832907bd1812e.png)
Mas a resposta é:
![2\left[x-3Ln\left(x+3 \right) \right]+c 2\left[x-3Ln\left(x+3 \right) \right]+c](/latexrender/pictures/40404a14eddf59cd1b7bd05341d6fd16.png)
Onde está meu erro?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Russman » Ter Ago 20, 2013 13:51
por Russman » Ter Ago 20, 2013 13:51
Sua resposta está certa! Veja que a constante

que surge no processo de integração é arbitrária. Isto é, pode ser qualquer uma. Assim, quando você efetua a multiplicação
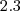
na sua resposta obtém o restante da função somado a um valor constante

que é absorvido pela própria constante

. Veja que isso só se pode fazer quando a constante for arbitrária.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Sobreira » Ter Ago 20, 2013 16:45
por Sobreira » Ter Ago 20, 2013 16:45
Deixa eu ver se entendi.
Na verdade ficaria 6+C, que resulta em outra C ??
Com relação a constante arbitrária significa que quando eu encontro uma solução que serve para uma família de funções esta constante pode ser arbitrária, enquanto que quando eu determino a constante eu estou determinando uma função específica?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Russman » Ter Ago 20, 2013 17:21
por Russman » Ter Ago 20, 2013 17:21
SIm,

é tão arbitrário quanto

.
Exatamente. Existe toda uma família de funções que quando derivadas resultam no integrando que você integrou. Isso se deve basicamente ao fato de que a derivada da função constante é nula e precisamos levar isso em conta. Assim, a constante que aparece representa essa propriedade e pode gerar não uma mas infinitas soluções para o mesmo problema de forma que a definimos como arbitrária.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Sobreira » Ter Ago 20, 2013 17:43
por Sobreira » Ter Ago 20, 2013 17:43
Muito Obrigado!!
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Sobreira » Qua Ago 21, 2013 12:23
por Sobreira » Qua Ago 21, 2013 12:23
Tratando ainda a respeito da questão de constantes, tenho esta dúvida:
Tendo por exemplo a seguinte equação diferencial:
![\frac{dy}{dx}=x\sqrt[]{y} \frac{dy}{dx}=x\sqrt[]{y}](/latexrender/pictures/77c5c8f47c4f749b0de05940df6daf64.png)
Resolvendo esta equação eu encontro como resposta uma família de funções:
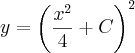
Logo, eu entendo que se eu determinar qualquer valor para a constante, esta função com esta constante será solução da equação diferencial. Ou seja se eu determino 0 para constante:
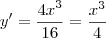
![\frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}} \frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}}](/latexrender/pictures/17a24a5b37c86eb319a075a6a2a6e74a.png)
Ou seja, esta função com esta constante é solução da E.D.O.
Entretanto se atribuo C=3 por exemplo:
![\frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}+9} \frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}+9}](/latexrender/pictures/d5de18b9b99c1046ae7590c012fef8ad.png)
Ou seja, esta função está dentro da família de soluções encontradas mas utilizando esta constante a equação não é satisfeita.
Onde estou errado?
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição / Integral por partes
por Carlos28 » Seg Out 19, 2015 12:25
- 1 Respostas
- 2948 Exibições
- Última mensagem por nakagumahissao

Seg Out 19, 2015 23:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição
por Aliocha Karamazov » Qui Fev 23, 2012 23:57
- 2 Respostas
- 2337 Exibições
- Última mensagem por MarceloFantini

Sex Fev 24, 2012 12:07
Cálculo: Limites, Derivadas e Integrais
-
- Integral (substituição)
por kika_sanches » Sex Mar 23, 2012 14:42
- 4 Respostas
- 2956 Exibições
- Última mensagem por kika_sanches

Sex Mar 23, 2012 15:35
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Dom Nov 18, 2012 10:46
- 1 Respostas
- 1744 Exibições
- Última mensagem por young_jedi

Dom Nov 18, 2012 10:54
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Seg Nov 19, 2012 16:23
- 7 Respostas
- 4366 Exibições
- Última mensagem por MarceloFantini

Ter Nov 20, 2012 21:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
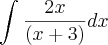
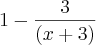 .
.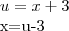
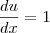

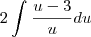
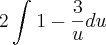
![2\left[u-3Lnu \right]+C 2\left[u-3Lnu \right]+C](/latexrender/pictures/7535c851fb47a911fb048a5531036424.png)
![2\left[\left(x+3 \right)-3Ln(x+3) \right]+C 2\left[\left(x+3 \right)-3Ln(x+3) \right]+C](/latexrender/pictures/7eb83629bc1824211cb832907bd1812e.png)
![2\left[x-3Ln\left(x+3 \right) \right]+c 2\left[x-3Ln\left(x+3 \right) \right]+c](/latexrender/pictures/40404a14eddf59cd1b7bd05341d6fd16.png)

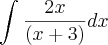
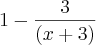 .
.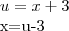
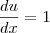

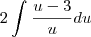
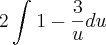
![2\left[u-3Lnu \right]+C 2\left[u-3Lnu \right]+C](/latexrender/pictures/7535c851fb47a911fb048a5531036424.png)
![2\left[\left(x+3 \right)-3Ln(x+3) \right]+C 2\left[\left(x+3 \right)-3Ln(x+3) \right]+C](/latexrender/pictures/7eb83629bc1824211cb832907bd1812e.png)
![2\left[x-3Ln\left(x+3 \right) \right]+c 2\left[x-3Ln\left(x+3 \right) \right]+c](/latexrender/pictures/40404a14eddf59cd1b7bd05341d6fd16.png)

 que surge no processo de integração é arbitrária. Isto é, pode ser qualquer uma. Assim, quando você efetua a multiplicação
que surge no processo de integração é arbitrária. Isto é, pode ser qualquer uma. Assim, quando você efetua a multiplicação 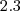 na sua resposta obtém o restante da função somado a um valor constante
na sua resposta obtém o restante da função somado a um valor constante  que é absorvido pela própria constante
que é absorvido pela própria constante  . Veja que isso só se pode fazer quando a constante for arbitrária.
. Veja que isso só se pode fazer quando a constante for arbitrária.

 é tão arbitrário quanto
é tão arbitrário quanto  .
.

![\frac{dy}{dx}=x\sqrt[]{y} \frac{dy}{dx}=x\sqrt[]{y}](/latexrender/pictures/77c5c8f47c4f749b0de05940df6daf64.png)
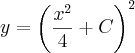
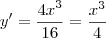
![\frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}} \frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}}](/latexrender/pictures/17a24a5b37c86eb319a075a6a2a6e74a.png)
![\frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}+9} \frac{{x}^{3}}{4}=x\sqrt[]{\frac{{x}^{4}}{16}+9}](/latexrender/pictures/d5de18b9b99c1046ae7590c012fef8ad.png)

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.