 com os eixos coordenados.
com os eixos coordenados.Se alguém puder dar dicas de como iniciar exercício, ficarei grato.

 com os eixos coordenados.
com os eixos coordenados.

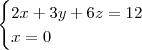
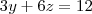 e
e 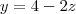 , que é uma reta. Os outros casos são semelhantes.
, que é uma reta. Os outros casos são semelhantes.

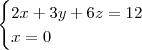
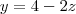
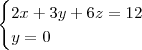
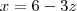
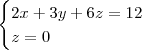
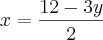
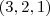



Claudin escreveu:Determine as interseções do planocom os eixos coordenados.
Se alguém puder dar dicas de como iniciar exercício, ficarei grato.
Russman escreveu:As equações dos eixos coordenados são, respectivamente, x=0, y=0 e z=0. As interssecções serão retas.
MarceloFantini escreveu:De uma certa forma, sim. Resolvendo o sistema
vem quee
, que é uma reta. Os outros casos são semelhantes.
 com o eixo x irá ocorrer quando x = t, y = 0 e z = 0. Substituindo esses valores na equação do plano obtemos t = 6. Portanto, o ponto de interseção do plano com o eixo x é (6, 0, 0).
com o eixo x irá ocorrer quando x = t, y = 0 e z = 0. Substituindo esses valores na equação do plano obtemos t = 6. Portanto, o ponto de interseção do plano com o eixo x é (6, 0, 0).

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

