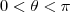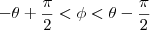por marinalcd » Sex Abr 19, 2013 11:48
por marinalcd » Sex Abr 19, 2013 11:48
Não estou conseguindo resolver este problema:
Seja S a superfície da esfera x²+y²+z²=a², situada no interior do cilindro x²+y² = ay, com a > 0. Determine o valor de a de modo que
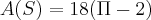
unidades de área.
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por young_jedi » Sex Abr 19, 2013 16:15
por young_jedi » Sex Abr 19, 2013 16:15
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por marinalcd » Sex Abr 19, 2013 16:42
por marinalcd » Sex Abr 19, 2013 16:42
Obrigada pelo auxílio!
Seguindo o seu raciocínio, estou resolvendo aqui, mas na hora de substituir na equação do cilindro o meu resultado deu diferente.
Acho que você só substituiu o valor de x. ...
Agora vou tentar resolver a integral!
Valeu!
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por young_jedi » Sex Abr 19, 2013 18:00
por young_jedi » Sex Abr 19, 2013 18:00
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por marinalcd » Seg Abr 22, 2013 20:32
por marinalcd » Seg Abr 22, 2013 20:32
Olá! Consegui fazer até a substituição na equação do cilindro e cheguei em:

Mas não entendi como você determinou os limites de integração. Não consegui sair dessa relação.
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por young_jedi » Ter Abr 23, 2013 11:19
por young_jedi » Ter Abr 23, 2013 11:19
então utilizando aqulea relação de seno e cosseno que eu coloquei voce chega em
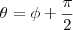
como se trata de um cilindro, pela simetria circular dele agente tem então que
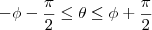
o o angulo
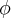
se determina pelo limite da esfera
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por marinalcd » Qua Abr 24, 2013 14:14
por marinalcd » Qua Abr 24, 2013 14:14
Eu costumo colocar o

determinado pelo limite da esfera.
Aí, para achar o
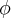
eu calculei o seno de teta (com os limites da esfera) e calculei a inversa do cossseno, encontrando assim os limites de
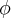
.
Pode ser assim? Pois deu diferente do seu, logo a integral dará diferente.
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por young_jedi » Qua Abr 24, 2013 14:42
por young_jedi » Qua Abr 24, 2013 14:42
a integral vai ser diferente, mais o valor final tem que ser igual
de qualquer forma faça do jeito que ficar mais facil pra voce visualizar os limites
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por marinalcd » Qua Abr 24, 2013 14:47
por marinalcd » Qua Abr 24, 2013 14:47
Só uma última coisa: na minha integral não aparece esse 2 multiplicando. Como você achou?
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por young_jedi » Qua Abr 24, 2013 14:49
por young_jedi » Qua Abr 24, 2013 14:49
esse 2 é porque essa integral é so para a parte de cima da esfera mais o cilindro corta a esfera na parte de baixo tambem sendo a area das duas partes identicas portanto multipliquei por 2
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por marinalcd » Sex Abr 26, 2013 18:00
por marinalcd » Sex Abr 26, 2013 18:00
Meu professor falou que deveria utilizar a variação de teta:

E que deveria por coordenadas esféricas a equação da interseção para encontrar a variação de
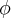
, que dependerá de

.
Mas ao substituir na equação, cheguei na seguinte relação:

E não consegui determinar a variação de \phi.
Não sei se fiz errado, mas não consegui chegar nessa variação que você chegou.
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por young_jedi » Sex Abr 26, 2013 18:19
por young_jedi » Sex Abr 26, 2013 18:19
eu não entendi como voce chegou nesta relação
de qualquer forma voce pode fazer a integral para
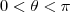
e
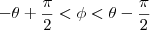
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6489 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4527 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2654 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5560 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
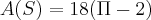 unidades de área.
unidades de área.
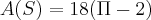 unidades de área.
unidades de área.
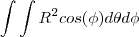
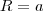

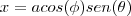

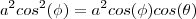


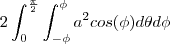


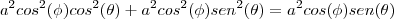
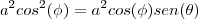
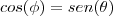
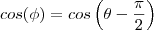
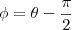
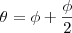
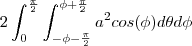



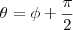
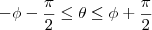
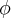 se determina pelo limite da esfera
se determina pelo limite da esfera
 determinado pelo limite da esfera.
determinado pelo limite da esfera. 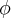 eu calculei o seno de teta (com os limites da esfera) e calculei a inversa do cossseno, encontrando assim os limites de
eu calculei o seno de teta (com os limites da esfera) e calculei a inversa do cossseno, encontrando assim os limites de 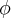 .
.




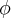 , que dependerá de
, que dependerá de  .
.