 por Fabio Cabral » Qua Out 13, 2010 13:03
por Fabio Cabral » Qua Out 13, 2010 13:03
Olá, galera. Voltei aqui para que me ajudem a terminar alguns exercícios para a prova, ok ?
vamos lá:
1. Aplicando propriedades de limites e algébricas, calcule cada limite abaixo e avalie sua existência, dizendo se eles existem ou não.
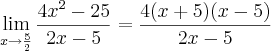
pois bem.
eu fiz isso certo ?
não estou conseguindo sair daí.
obrigado.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Neperiano » Qua Out 13, 2010 16:52
por Neperiano » Qua Out 13, 2010 16:52
Ola
Corte o 2 debaixo com o 4 de cima, depois é so cortar o x-5 de cima com o debaixo
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Fabio Cabral » Qua Out 13, 2010 17:46
por Fabio Cabral » Qua Out 13, 2010 17:46
Eu consegui resolver, mas a resposta deu 15 sendo que o certo seria 10. pode me ajudar?
segue o que eu fiz:

Será que eu errei na simplificação ?
Grato.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Qua Out 13, 2010 18:33
por Fabio Cabral » Qua Out 13, 2010 18:33
Grande Fantini. Obrigado novamente.
Aproveitando o tópico, vou tirar todas as dúvidas aqui. consegui fazer 20 questões de 60. Ta devagar mas ta indo. rs
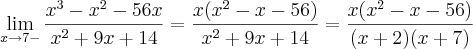
dai eu não consigo sair pois quando faço báscara para calcular as raízes do numerador, o resultado indica que não possui raízes.
corrija-me se estiver errado. A resposta = 0.
ps.: desculpa o tanto de perguntas, é que estou tentando enteder tudo..
Grato.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Qua Out 13, 2010 20:34
por Fabio Cabral » Qua Out 13, 2010 20:34
Nooossa, que mancada que eu dei. Falta de atenção. Errei um sinal..
Obrigado novamente.
Com essas questões que você me tira as dúvidas, consigo fazer em média 4/5 outras questões, to caminhando bem.
la vai outra:
![\lim_{x\rightarrow0} \frac{\sqrt[2]{7+t}-\sqrt[2]{7}}{t} \lim_{x\rightarrow0} \frac{\sqrt[2]{7+t}-\sqrt[2]{7}}{t}](/latexrender/pictures/ca8b84128311d3d0088f0632f2302c39.png)
Eu tentei fazer aqui de acordo com o que eu sei, e consegui achar 1/14. Mas não sei se esta certo.

" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Elcioschin » Qua Out 13, 2010 22:41
por Elcioschin » Qua Out 13, 2010 22:41
Multiplique o numerador e o denominador pelo conjugado V(7 + t) + V7
No numerador se obtém (7 + t) - 7 = t
Simplifique t do numerador e do denominador
Sobra no denominador V(7 + t) + 7
Fazendo t = 0 o denominador fica ----> 2*V7
1/2*V7 = V7/14
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Fabio Cabral » Qui Out 14, 2010 09:43
por Fabio Cabral » Qui Out 14, 2010 09:43
Entendo. Mas acho que tem algo errado.
A resposta está como
![\frac{1}{14}\sqrt[]{7} \frac{1}{14}\sqrt[]{7}](/latexrender/pictures/a836a2ab4bcaea3cdc6945fed62b229c.png)
:(
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Elcioschin » Qui Out 14, 2010 14:26
por Elcioschin » Qui Out 14, 2010 14:26
Exatamente a minha resposta: a letra V significa "raiz quadrada".
E é óbvio que 1*V7 = V7
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Fabio Cabral » Seg Out 18, 2010 09:26
por Fabio Cabral » Seg Out 18, 2010 09:26
Obrigado novamente.
Vamos lá.
Surgiu uma dúvida aqui.

Ta certo esse meu desenvolvimento? A resposta seria -? ou +?.
deduzi como :

Grato.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5414 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4760 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4786 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4813 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2797 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
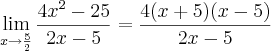

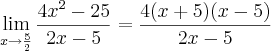





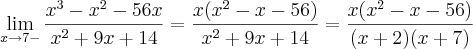

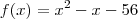
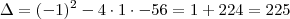
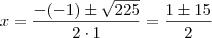
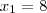




![\lim_{x\rightarrow0} \frac{\sqrt[2]{7+t}-\sqrt[2]{7}}{t} \lim_{x\rightarrow0} \frac{\sqrt[2]{7+t}-\sqrt[2]{7}}{t}](/latexrender/pictures/ca8b84128311d3d0088f0632f2302c39.png)


![\frac{1}{14}\sqrt[]{7} \frac{1}{14}\sqrt[]{7}](/latexrender/pictures/a836a2ab4bcaea3cdc6945fed62b229c.png)





 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.