Encontre p e q tais que g seja contínua e diferenciável em
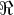 .Justifique a sua resposta.
.Justifique a sua resposta.(Lembre que uma função f é diferenciável em Dom(f) se existe f'(x) para todo x
 Dom(f).)
Dom(f).)g(x)= 6x+1 ,se x<3 e
px²+qx ,se x
 3
3
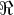 .Justifique a sua resposta.
.Justifique a sua resposta. Dom(f).)
Dom(f).) 3
3
 quando
quando 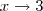 sejam iguais, já que
sejam iguais, já que  é, por alto, abscissa do único possível ponto de descontinuidade.
é, por alto, abscissa do único possível ponto de descontinuidade.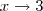 pela esquerda:
pela esquerda: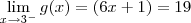 ; esse deve ser o limite quando
; esse deve ser o limite quando 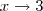 pela direita, isto é:
pela direita, isto é: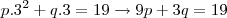
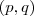 que tornam a função diferenciável formam uma reta de equação
que tornam a função diferenciável formam uma reta de equação 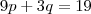


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: