Bom dia pessoal (especialmente ao Sr. Molina, que responde com muita presteza!).
Já tinha feito uma questão parecida com esta, mas não entendi o enunciado, pois ele pergunta quantos quilômetros serão percorridos. Mas por quem?
Segue o enunciado:
O caminho A tem 1km de extensão, B tem 1,2 km, C tem 1,5 km, D tem 2 km e E tem 3 km. Antônio vai dar voltas pelo caminho A, Bernardo por B, Carlos por C, Daniel por D e Edson pelo caminho E. Todos vão sair de O no mesmo instante e caminhar com a mesma velocidade. Os cinco chegarão de novo no ponto O, ao mesmo tempo, depois de percorrerem a seguinte distância, em quilômetros: ?
Só para informar, a resposta correta é 6km. (Mas o que significa esses 6km? A distância que algum caminhou? A soma das distâncias de todos - que não dá; A distância daquele que caminhou mais?
Pensei assim:
A - 1,0
B = 1,2
C = 1,5
D = 2,0
E = 3
Nesse caso, nenhum passa pelo ponto O. Por exemplo, ninguém chegará junto antes de o E ter completado, ou seja, o mínimo a ser percorrido pelo E teria que ser 3.
Mas o D já terá caminhado 1km a mais (segunda volta)
Aí somei uma volta para cada (esta são as distâncias de cada um após a segunda volta):
A = 1,0 => 2,0
B = 1,2 => 2,4
C = 1,5 => 3,0
D = 2,0 => 4,0
E = 3,0 => 6,0
O A, o C e o E chegariam juntos. Mas se são 6km a resposta certa, o B, nesse caso, teria passado 400m... E o "E" já percorreu 6km... O "D" já teria passado 1km (segunda volta...)
Não consegui me fazer entender...
Obrigado a todos pela ajuda!


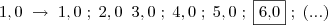
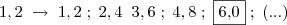
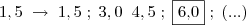
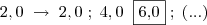


 .
.
 :
: