 por studieren » Qua Abr 28, 2010 17:08
por studieren » Qua Abr 28, 2010 17:08
Estou estudando por conta própria com alguns materiais que tenho, e então surgiu dúvidas no decurso dos estudos.
A primeira imagem trata-se de uma página do livro Fundamentos de Matemática Elementar, Vol. 1
http://img690.imageshack.us/img690/7982/digitalizar0004q.jpgQuanto aos exemplos, não sei se foi problema de interpretação minha ou se foi erro de diagramação do livro. Na parte esquerda, o gráfico de
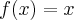
,

e
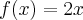
aparecem iguais.
A segunda imagem trata-se de uma apostila que eu ganhei de uma amiga, sobre a explicação de um exercício sobre função inversa.
http://img706.imageshack.us/img706/5070/digitalizar0007.jpg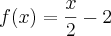
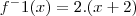
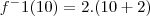
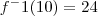
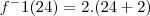
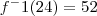
Mas por que a resolução do exemplo da apostila é
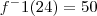
?
Valeu !
-
studieren
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jan 01, 2010 22:34
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qua Abr 28, 2010 18:56
por MarceloFantini » Qua Abr 28, 2010 18:56
Acredito que esteja errado a conta do exemplo, o seu raciocínio está certo.
Sobre a primeira imagem, não entendi qual a sua dúvida?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por studieren » Qui Abr 29, 2010 01:01
por studieren » Qui Abr 29, 2010 01:01
Minha dúvida é que a reta da função
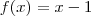
deveria cortar a coordenada e a abscissa, e não o centro do gráfico.
Por que os gráficos de cada uma das três funções são esboçados com semelhança ?
-
studieren
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jan 01, 2010 22:34
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Abr 29, 2010 17:59
por MarceloFantini » Qui Abr 29, 2010 17:59
Deveria, mas não se preocupe tanto com os gráficos se você entendeu os conceitos claramente. São exemplos particulares, e o importante é que você aprenda o conceito para aplicar para qualquer função.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por studieren » Sáb Mai 01, 2010 18:31
por studieren » Sáb Mai 01, 2010 18:31
Beleza ! Valeu pela explicação.
-
studieren
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jan 01, 2010 22:34
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função inversa - dúvida
por laura_biscaro » Qua Abr 10, 2013 23:00
- 1 Respostas
- 1342 Exibições
- Última mensagem por young_jedi

Qui Abr 11, 2013 11:53
Funções
-
- Duvida com Função Inversa
por pedro_nog » Dom Jul 27, 2014 21:42
- 1 Respostas
- 1522 Exibições
- Última mensagem por young_jedi

Qua Jul 30, 2014 17:33
Funções
-
- [Matrizes] Dúvida conceitual
por souzalucasr » Qua Ago 22, 2012 14:26
- 4 Respostas
- 4846 Exibições
- Última mensagem por souzalucasr

Qua Ago 29, 2012 12:34
Matrizes e Determinantes
-
- Dúvida - resolução(função inversa)
por jamiel » Ter Jun 14, 2011 18:49
- 1 Respostas
- 1476 Exibições
- Última mensagem por DanielFerreira

Qui Jun 16, 2011 16:00
Funções
-
- Dúvida conceitual sobre funções.
por Sobreira » Seg Fev 25, 2013 22:29
- 1 Respostas
- 1629 Exibições
- Última mensagem por Russman

Ter Fev 26, 2013 02:15
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
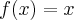 ,
,  e
e 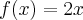 aparecem iguais.
aparecem iguais.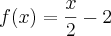
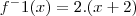
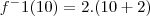
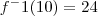
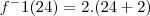
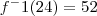
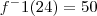 ?
?



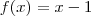 deveria cortar a coordenada e a abscissa, e não o centro do gráfico.
deveria cortar a coordenada e a abscissa, e não o centro do gráfico. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
