 por adauto martins » Qua Out 23, 2019 20:56
por adauto martins » Qua Out 23, 2019 20:56
(EN-escola naval-exame?)
sejam f e g duas funçoes reais e derivaveis tais que
![f'(x)=sen(cos\sqrt[]{x}) f'(x)=sen(cos\sqrt[]{x})](/latexrender/pictures/c68c7e3e709155d641110f4a8caff361.png)
e
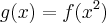
,
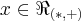
.pode-se afirmar
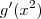
é igual a:
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qua Out 23, 2019 21:12
por adauto martins » Qua Out 23, 2019 21:12
soluçao:
pelos dados do problema,temos que:
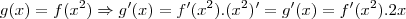
,
aqui usando a "regra da cadeia das funçoes compostas"...logo:
![g'(x)=f'({x}^{2}).2x=f'(sen(cos\sqrt[]{({x}^{2})}).2x
g'(x)=f'(sen(cosx)).2x g'(x)=f'({x}^{2}).2x=f'(sen(cos\sqrt[]{({x}^{2})}).2x
g'(x)=f'(sen(cosx)).2x](/latexrender/pictures/a30d15e98866d3e7f98d79a8aa917fab.png)
...
portanto:
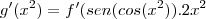
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f'(x)=sen(cos\sqrt[]{x}) f'(x)=sen(cos\sqrt[]{x})](/latexrender/pictures/c68c7e3e709155d641110f4a8caff361.png) e
e 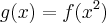 ,
,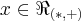 .pode-se afirmar
.pode-se afirmar 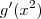 é igual a:
é igual a:
![f'(x)=sen(cos\sqrt[]{x}) f'(x)=sen(cos\sqrt[]{x})](/latexrender/pictures/c68c7e3e709155d641110f4a8caff361.png) e
e 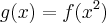 ,
,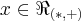 .pode-se afirmar
.pode-se afirmar 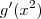 é igual a:
é igual a:
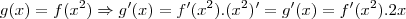 ,
,![g'(x)=f'({x}^{2}).2x=f'(sen(cos\sqrt[]{({x}^{2})}).2x
g'(x)=f'(sen(cosx)).2x g'(x)=f'({x}^{2}).2x=f'(sen(cos\sqrt[]{({x}^{2})}).2x
g'(x)=f'(sen(cosx)).2x](/latexrender/pictures/a30d15e98866d3e7f98d79a8aa917fab.png) ...
...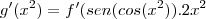


 .
.
 :
: