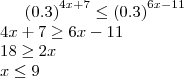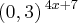
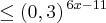
Ok, esta questão é simples, mas exige um pouco de cuidado.
A primeira vista tendemos a querer "cortar" o 0,3 nos dois lados e fazer
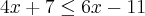
, mas estaria incorreto.
Observe que a base (0.3 ou 3/10) é fracionaria, portanto ao "cortarmos" esta base, o sinal da inequação deve ser invertido, veja:
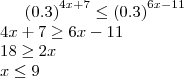
O porque disso é simples, quando elevamos uma fração a um expoente positivo qualquer, ao invés de o resultado ser um numero maior, ele será um numero menor.
ex.: (0.5)^2 = 0.25 ; (0.5)^3 = 0.125
Sendo assim para respeitar a inequação invertemos o seu sentido, ou seja, para o termo da esquerda ser menor/igual que o da direita, seu expoente deve ser maior/igual que o da direita.
Espero ter ajudado, qualquer duvida é só perguntar.
Bons estudos.
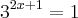 =(2x+1)ln(3)=0 2x+1=0 2x=-1 x=-1/2
=(2x+1)ln(3)=0 2x+1=0 2x=-1 x=-1/2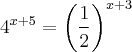 =(2^2)^x+5=(12)2x+3=(2^2)x+5=(2-1)2x+3
=(2^2)^x+5=(12)2x+3=(2^2)x+5=(2-1)2x+3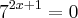 sem solução porque vai dar negativo/x e não pode ser negativo
sem solução porque vai dar negativo/x e não pode ser negativo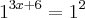 3x+6=2 x=-43
3x+6=2 x=-43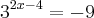 sem solução porque vai dar negativo/x e não pode ser negativo
sem solução porque vai dar negativo/x e não pode ser negativo



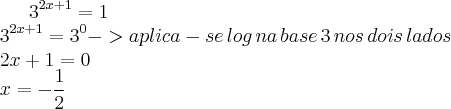


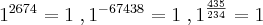 ).
). 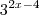 ou uma base negativa (-4^2x-4, por exemplo), este termo nunca poderá assumir um valor negativo.
ou uma base negativa (-4^2x-4, por exemplo), este termo nunca poderá assumir um valor negativo.  .
.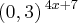
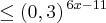
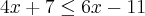 , mas estaria incorreto.
, mas estaria incorreto.