 por Pessoa Estranha » Ter Nov 18, 2014 00:38
por Pessoa Estranha » Ter Nov 18, 2014 00:38
Olá, pessoal! Preciso de ajuda para o seguinte exercício: "Determinar onde o gráfico da função dada tem concavidade positiva, onde a concavidade é negativa e obter os pontos de inflexão, caso existam."
![\sqrt[5]{x-2} \sqrt[5]{x-2}](/latexrender/pictures/3077b32665829a49219836be64d5ac4d.png)
Fiz o seguinte:
Derivei duas vezes a função dada, chegando à:
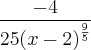
. Daí, não há pontos reais para os quais a derivada segunda da f se anula. Contudo, x = 2 está no domínio da f e é, realmente, a abscissa do ponto de inflexão, mas como chegar neste resultado usando as derivadas e sem observar o gráfico da f? Pq não deu certo?
Por favor, eu preciso muito de ajuda!
Muito Obrigada!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Qua Nov 19, 2014 11:46
por adauto martins » Qua Nov 19, 2014 11:46
![f(x)=\sqrt[5]{x-2}=0\Rightarrow x=2 f(x)=\sqrt[5]{x-2}=0\Rightarrow x=2](/latexrender/pictures/ea0c85a502ea218a13a208284cf1a0ff.png)
,x=2 e o ponto onde f,cruza o eixo xx...
![df/dx=(1/5)1/(\sqrt[5]{{x-2}^{4}})=0\Rightarrow df/dx=(1/5)1/(\sqrt[5]{{x-2}^{4}})=0\Rightarrow](/latexrender/pictures/dfb72ab60de1da46a82ae0ce046cfa4a.png)
nao existem pontos nem de maximos e minimos,mas a funçao e crescente,pois
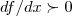
,p/ qquer x do dominio,

...
![({df/dx})^{2}=(-4/25)(\sqrt[5]{({x-2})^{9}})=0 ({df/dx})^{2}=(-4/25)(\sqrt[5]{({x-2})^{9}})=0](/latexrender/pictures/2c0f115f91028ad44ed6806e741b495c.png)

q. nao tem concavidades...portanto f e uma funçao sem pontos criticos,mas cresce indefinidamente,pois
![\lim_{x\rightarrow\infty}(\sqrt[5]{x-2})=\infty \lim_{x\rightarrow\infty}(\sqrt[5]{x-2})=\infty](/latexrender/pictures/12ec7e0fbcdd23d3bd585d69a80a9dfc.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por trickpsv » Sex Nov 21, 2014 16:06
por trickpsv » Sex Nov 21, 2014 16:06
Bem, não podemos esquecer que ponto de inflexâo é onde a função muda de concavidade, e não necessariamente onde a segunda derivada é 0, ela pode também não existir.
Analisando o gráfico da função dada vemos claramente que a função muda de concavidade no ponto x=2. Utilizando a derivada de ordem 2, basta verificar se há algum ponto onde ela é igual a 0 ou ela onde não está definida, nesse caso x=2.
Depois basta tomar um valor menor que 2 para x e outro maior que 2 e verificar se mudou o sinal da segunda derivada, se sim, é ponto de inflexão.
-
trickpsv
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Nov 21, 2014 15:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por adauto martins » Sex Nov 21, 2014 17:01
por adauto martins » Sex Nov 21, 2014 17:01
aqui e vc lembrar de cinematica...qdo o movel muda p/uma direçao inversa,sua velocidade tem q. ser nula e consequentemente sua aceleraçao...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] Concavidade e pontos de Inflexão
por fabriel » Sex Set 21, 2012 22:56
- 3 Respostas
- 2449 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 01:18
Cálculo: Limites, Derivadas e Integrais
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3390 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
-
- Ponto de Inflexão
por Kelvin Brayan » Ter Mai 24, 2011 16:21
- 3 Respostas
- 2739 Exibições
- Última mensagem por Fabio Cabral

Ter Jun 07, 2011 13:29
Funções
-
- [derivada] Ponto minimo/máximo e concavidade
por gabriel feron » Dom Out 07, 2012 03:52
- 1 Respostas
- 2204 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 10:56
Cálculo: Limites, Derivadas e Integrais
-
- [AJUDA] Derivada: Ponto Máx, Minimo, Inflexão e Assíntota
por Mateus Leao » Qua Mai 16, 2012 13:03
- 2 Respostas
- 2393 Exibições
- Última mensagem por ricardosanto

Sex Mai 18, 2012 19:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[5]{x-2} \sqrt[5]{x-2}](/latexrender/pictures/3077b32665829a49219836be64d5ac4d.png)
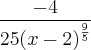 . Daí, não há pontos reais para os quais a derivada segunda da f se anula. Contudo, x = 2 está no domínio da f e é, realmente, a abscissa do ponto de inflexão, mas como chegar neste resultado usando as derivadas e sem observar o gráfico da f? Pq não deu certo?
. Daí, não há pontos reais para os quais a derivada segunda da f se anula. Contudo, x = 2 está no domínio da f e é, realmente, a abscissa do ponto de inflexão, mas como chegar neste resultado usando as derivadas e sem observar o gráfico da f? Pq não deu certo?

![f(x)=\sqrt[5]{x-2}=0\Rightarrow x=2 f(x)=\sqrt[5]{x-2}=0\Rightarrow x=2](/latexrender/pictures/ea0c85a502ea218a13a208284cf1a0ff.png) ,x=2 e o ponto onde f,cruza o eixo xx...
,x=2 e o ponto onde f,cruza o eixo xx...![df/dx=(1/5)1/(\sqrt[5]{{x-2}^{4}})=0\Rightarrow df/dx=(1/5)1/(\sqrt[5]{{x-2}^{4}})=0\Rightarrow](/latexrender/pictures/dfb72ab60de1da46a82ae0ce046cfa4a.png) nao existem pontos nem de maximos e minimos,mas a funçao e crescente,pois
nao existem pontos nem de maximos e minimos,mas a funçao e crescente,pois 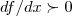 ,p/ qquer x do dominio,
,p/ qquer x do dominio, ...
...![({df/dx})^{2}=(-4/25)(\sqrt[5]{({x-2})^{9}})=0 ({df/dx})^{2}=(-4/25)(\sqrt[5]{({x-2})^{9}})=0](/latexrender/pictures/2c0f115f91028ad44ed6806e741b495c.png)
 q. nao tem concavidades...portanto f e uma funçao sem pontos criticos,mas cresce indefinidamente,pois
q. nao tem concavidades...portanto f e uma funçao sem pontos criticos,mas cresce indefinidamente,pois ![\lim_{x\rightarrow\infty}(\sqrt[5]{x-2})=\infty \lim_{x\rightarrow\infty}(\sqrt[5]{x-2})=\infty](/latexrender/pictures/12ec7e0fbcdd23d3bd585d69a80a9dfc.png) ...
...
