 por pedro_kampos » Dom Ago 03, 2014 20:34
por pedro_kampos » Dom Ago 03, 2014 20:34
Pessoal, tentei solucionar essa questão mas não consigo achar a preposição correta. e não bate com meus calculos:

Minha humilde resolucao:

-
pedro_kampos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Jul 14, 2014 04:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia da computacao
- Andamento: cursando
 por adauto martins » Sáb Nov 08, 2014 11:14
por adauto martins » Sáb Nov 08, 2014 11:14
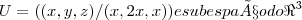
;W=(1,0-1) e um ponto do {\Re}^{3}...
como U+W e subespaço do
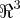
,entao:
U+W e um subespaço do
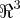
,entao :U+W=(x+1,2x,x),
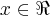
U+W=0
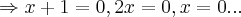
o q. contradiz pois x=-1 e x=0...logo U+W nao e subespaço do
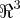
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Sáb Nov 08, 2014 13:55
por e8group » Sáb Nov 08, 2014 13:55
Cuidado ! Soma de quaisquer dois (ou qualquer quantidade finita ) subespaços de um mesmo espaço vetorial é sempre um subespaço do espaço em questão , a prova é bem relativamente simples e a generalização entre parêntesis é assegurada por indução .
Em relação ao exercício , os dois subespaços são retas no R^3 que passam pela origem , e assim a base de tais subespaços constituem apenas de um vetor , como já foi verificado acima
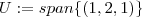
e pelo enunciado
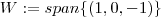
.
Temos que
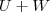
é subespaço do
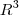
e assim um vetor arbitrário deste subespaço é
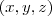
que se exprime como soma de dois vetores
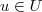
e

, e estes vetores são dados por
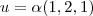
e

. Segue daí que
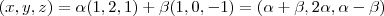
. Logo
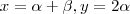
e
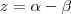
e por isso (soma x + z e substitui 2 alpha por y )

, pedro sua resposta está certa , porém confuso .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por adauto martins » Sáb Nov 08, 2014 14:27
por adauto martins » Sáb Nov 08, 2014 14:27
tudo bem santiago...mas nao concordo com seus argumentos...o presente execicio,somente traz o vetorW=(1,0-1)q. na verdade e um ponto no espaço e nao esta contido no subespaço U...um ponto q. nao seja a origem ,nao e subespaço por si so...a origem sim,e unico,como e facil demonstrar...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por e8group » Sáb Nov 08, 2014 15:43
por e8group » Sáb Nov 08, 2014 15:43
Caro adauto martins parece que tem alguns livros que utiliza a notação [ M ] (onde M é conjunto de elementos de um E.V) para designar o conjunto de todas combinações lineares possível dos elementos de M . Por exemplo , sendo
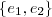
a base canônica para o
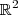
, de acordo com a notação acima
![\mathbb{R}^2 = [\{e_1 , e_2 \} ] \mathbb{R}^2 = [\{e_1 , e_2 \} ]](/latexrender/pictures/eab37dffaff4c2dc5911c50bdb67a424.png)
.Eu particularmente evito esta notação e simplesmente escrevo
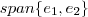
ou
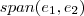
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Algebra Linear] Soma de subespaços
por pedro_kampos » Dom Ago 03, 2014 20:19
- 1 Respostas
- 2529 Exibições
- Última mensagem por adauto martins

Seg Nov 10, 2014 16:02
Álgebra Linear
-
- [Álgebra Linear]-Interseção de subespaços
por Ana_Rodrigues » Ter Mai 08, 2012 23:19
- 1 Respostas
- 2323 Exibições
- Última mensagem por MarceloFantini

Qua Mai 09, 2012 21:34
Álgebra Linear
-
- Algebra Linear: Igualdade de Subespaços vetoriais
por leandro_aur » Ter Nov 01, 2011 05:40
- 1 Respostas
- 3642 Exibições
- Última mensagem por MarceloFantini

Ter Nov 01, 2011 15:21
Álgebra
-
- Subespaços Vetoriais
por felipe_ad » Sex Ago 27, 2010 19:56
- 1 Respostas
- 2299 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 28, 2010 19:31
Geometria Analítica
-
- Subespaços vetoriais
por ewald » Seg Mar 26, 2012 03:50
- 6 Respostas
- 4381 Exibições
- Última mensagem por LuizAquino

Qui Mar 29, 2012 13:26
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






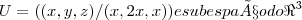 ;W=(1,0-1) e um ponto do {\Re}^{3}...
;W=(1,0-1) e um ponto do {\Re}^{3}...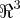 ,entao:
,entao: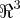 ,entao :U+W=(x+1,2x,x),
,entao :U+W=(x+1,2x,x),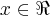
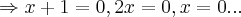 o q. contradiz pois x=-1 e x=0...logo U+W nao e subespaço do
o q. contradiz pois x=-1 e x=0...logo U+W nao e subespaço do 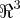

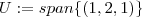 e pelo enunciado
e pelo enunciado 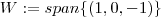 .
.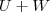 é subespaço do
é subespaço do 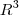 e assim um vetor arbitrário deste subespaço é
e assim um vetor arbitrário deste subespaço é 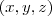 que se exprime como soma de dois vetores
que se exprime como soma de dois vetores 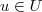 e
e  , e estes vetores são dados por
, e estes vetores são dados por 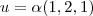 e
e  . Segue daí que
. Segue daí que 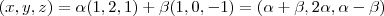 . Logo
. Logo 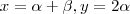 e
e 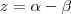 e por isso (soma x + z e substitui 2 alpha por y )
e por isso (soma x + z e substitui 2 alpha por y ) , pedro sua resposta está certa , porém confuso .
, pedro sua resposta está certa , porém confuso .

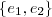 a base canônica para o
a base canônica para o 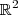 , de acordo com a notação acima
, de acordo com a notação acima ![\mathbb{R}^2 = [\{e_1 , e_2 \} ] \mathbb{R}^2 = [\{e_1 , e_2 \} ]](/latexrender/pictures/eab37dffaff4c2dc5911c50bdb67a424.png) .Eu particularmente evito esta notação e simplesmente escrevo
.Eu particularmente evito esta notação e simplesmente escrevo 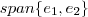 ou
ou 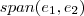 .
.