f(x,y) =arctg (y/x) no ponto p =(x,y), sendo x ? 0 ?
Até compreendo a noção de derivadas parciais, mas tenho extrema dificuldade em exemplos que envolvam arco-tangente (arctg).



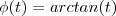 , equivalentemente
, equivalentemente 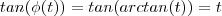 .
. ![[tan( arctan(t))]' = tan'(arctan(t)) \cdot \phi'(t) = t' = 1 [tan( arctan(t))]' = tan'(arctan(t)) \cdot \phi'(t) = t' = 1](/latexrender/pictures/44e429ead90e1a579c47a69654e55565.png) (no lado esquerdo vc derivada a função tangente e avalia ela em
(no lado esquerdo vc derivada a função tangente e avalia ela em 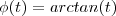 ) sse
) sse 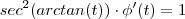 sse
sse ![[tan^2(arctan(t)) +1] \cdot phi'(t) = 1 [tan^2(arctan(t)) +1] \cdot phi'(t) = 1](/latexrender/pictures/55b4dd458d8f28e96b6a6ac1a512eece.png) sse
sse 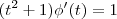 sse
sse 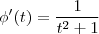 .
.  qualquer função real de uma variável . Agora derivamos pela regra da composta ,
qualquer função real de uma variável . Agora derivamos pela regra da composta , ![[\phi(g(t))]' = \phi'(g(t)) \cdot g'(t) = \frac{g'(t)}{1+[g(t)]^2} (*) [\phi(g(t))]' = \phi'(g(t)) \cdot g'(t) = \frac{g'(t)}{1+[g(t)]^2} (*)](/latexrender/pictures/5921beeb29fc2fe73238f0899abf8db9.png) .
. 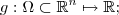 . Para cada
. Para cada 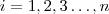 ,fixamos
,fixamos 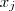 sobre todos índices distintos de i entre 1 e n e fazemos
sobre todos índices distintos de i entre 1 e n e fazemos 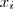 variar-se .
variar-se . 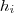 de uma variável a qual depende de x_i ( suponha que classe C^1 , diferenciável ) . Temos
de uma variável a qual depende de x_i ( suponha que classe C^1 , diferenciável ) . Temos 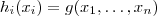 . Logo , derivar-se parcialmente
. Logo , derivar-se parcialmente 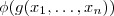 com respeito à
com respeito à 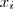 corresponde a derivar via regra da cadeia a expressão
corresponde a derivar via regra da cadeia a expressão 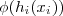 xom respeito à x_i . Portanto a fórmula (*) é válida .
xom respeito à x_i . Portanto a fórmula (*) é válida .

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.