 por urso » Ter Abr 22, 2014 11:08
por urso » Ter Abr 22, 2014 11:08
Buenas galera!
Estou com duvida nesta questão, não sei se para resolver ela, não sei se preciso pegar os pontos em x e y para ver se é continua e se preciso derivar para encontrar a diferenciabilidade.

Tenho mais 2 questões nesse estilo, qualquer coisa posto aqui para tirar as duvidas depois que vocês me derem uma luz nessa! Vlw!

-
urso
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 22, 2014 10:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Mec
- Andamento: cursando
 por urso » Ter Abr 22, 2014 15:58
por urso » Ter Abr 22, 2014 15:58
Bom galera, acho que consegui resolver!
Eu fiz os limites e descobri:
f(1) = -2.1+4 = 2
f(1) = -2.1+5 = 3
Como os limites não são iguais, o limite bilateral não existe consequentemente não é diferenciavel em x=1.
Tudo certo até aqui, mas se a questão tivesse limite bilateral, o que eu faço? Derivo? Para isso trouxe a tona mais 2 questões, preciso de ajuda nelas!

-
urso
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 22, 2014 10:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Mec
- Andamento: cursando
 por e8group » Qua Abr 23, 2014 11:18
por e8group » Qua Abr 23, 2014 11:18
Polinômios definidos em um intervalo aberto são sempre diferenciáveis .
Considere
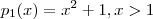
e
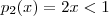
.
Como ambos polinômios estão definidos em intervalos abertos , logo eles são diferenciáveis .Assim , usando que diferenciabilidade implica continuidade já podemos afirmar que a função

é contínua em
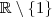
.Agora vamos mostrar que

é diferenciável em x = 1 e com isso concluir que f é contínua .
Por definição ,
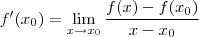
desde que o limite exista . E quando o limite existe ? Quando os limites laterais de f são números reais e são iguais .
Assim ,
(i)
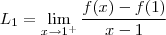
.Como estamos trabalhando com

então
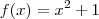
.Segue
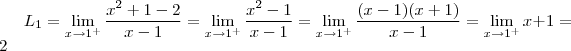
.
(ii)
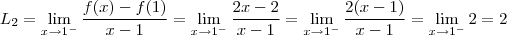

é diferenciável em x = 1 .Só por curiosidade f é diferenciável em toda reta .
OBS.: Só para efeito de organização (vide regras do fórum ) evite postar mais de uma dúvida em um único tópico , uma dúvida para cada tópico . Além disso , anexe imagens somente se for necessário . Neste caso pode usar o LaTeX para digitar suas expressões .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por urso » Qua Abr 23, 2014 12:24
por urso » Qua Abr 23, 2014 12:24
Bom dia Santhiago! Obrigado pela resposta

, foi de grande valia!
Grato,
-
urso
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Abr 22, 2014 10:58
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Mec
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo I - Gráfico
por Hel » Sáb Jan 09, 2010 15:52
- 0 Respostas
- 1928 Exibições
- Última mensagem por Hel

Sáb Jan 09, 2010 15:52
Cálculo: Limites, Derivadas e Integrais
-
- Calculo 1: Grafico
por Piva » Qua Jun 29, 2011 19:13
- 0 Respostas
- 1412 Exibições
- Última mensagem por Piva

Qua Jun 29, 2011 19:13
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] esboço de gráfico
por beel » Ter Nov 01, 2011 16:16
- 1 Respostas
- 2168 Exibições
- Última mensagem por LuizAquino

Ter Nov 01, 2011 16:29
Cálculo: Limites, Derivadas e Integrais
-
- cálculo 1 gráfico da função
por ezidia51 » Dom Set 29, 2019 19:53
- 2 Respostas
- 6311 Exibições
- Última mensagem por ezidia51

Seg Set 30, 2019 17:28
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Lei da função a partir do grafico
 por deosdete » Dom Jun 10, 2012 16:29
por deosdete » Dom Jun 10, 2012 16:29
- 4 Respostas
- 3310 Exibições
- Última mensagem por LuizAquino

Ter Jun 12, 2012 12:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





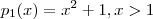 e
e 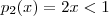 .
. é contínua em
é contínua em  .Agora vamos mostrar que
.Agora vamos mostrar que 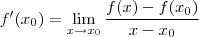 desde que o limite exista . E quando o limite existe ? Quando os limites laterais de f são números reais e são iguais .
desde que o limite exista . E quando o limite existe ? Quando os limites laterais de f são números reais e são iguais . 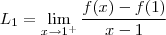 .Como estamos trabalhando com
.Como estamos trabalhando com  então
então 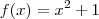 .Segue
.Segue 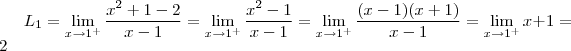 .
.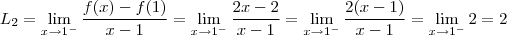
 é diferenciável em x = 1 .Só por curiosidade f é diferenciável em toda reta .
é diferenciável em x = 1 .Só por curiosidade f é diferenciável em toda reta . 
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.