 por e8group » Sex Jan 03, 2014 12:32
por e8group » Sex Jan 03, 2014 12:32
Já tentou obter a interseção entre elas ?

. Na primeira volta , os ângulos cujo seno vale 1/2 são

e

. Tente esboçar as curvas . Pelo esboço das curvas você consegue concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pessoa Estranha » Sex Jan 03, 2014 14:51
por Pessoa Estranha » Sex Jan 03, 2014 14:51
No caso de coordenadas polares, eu não sei como fazer. Fiz um esboço das duas curvas, mas em coordenadas polares. Para calcular a interseção entre ambas, não consigo entender o que fazer. Sei que deve aplicar integral, mas como fazer isto para um determinado intervalo, sendo que temos um desenho como, a grosso modo, uma "circunferência", ou melhor, curvas semelhantes ao cardióide. Não sei se estou escrevendo absurdos, mas é isso....

Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Sex Jan 03, 2014 15:26
por Pessoa Estranha » Sex Jan 03, 2014 15:26
Seria calcular:
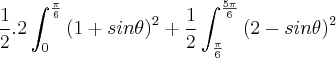
?
Se for assim, então acho que entendi!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sex Jan 03, 2014 16:18
por e8group » Sex Jan 03, 2014 16:18
A respeito do cálculo do integral não tenho 100% de certeza o que vou dizer se está certo . A respeito das interseções entre ambas curvas ,pode ser obtida conforme fazemos com as curvas no plano xy ,estas curvas estão no plano

. Cada uma destas curvas podem ser descritas pelos subconjuntos do plano

,que são

e

. A interseção entre as duas curvas é descrita pelo conjunto ,

.Logo ,

sse

e

sse

e

... Acredito que isto responde a sua dúvida
Pessoa Estranha escreveu: Para calcular a interseção entre ambas, não consigo entender o que fazer.
PS.: Troquei rho por r e theta por t apenas por simplicidade .
Se impormos que t (theta) varia em
![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png)
, e digitando
" area between the curves r = 2 - sin (t) and r= 1 + sin (t) , from t = 0 to 2pi " lá no wolfram alpha ,ele computa a área .
A grosso modo, na minha opinião , esboçando as curvas é possível ver quem esta acima e abaixo em um determinado intervalo
![\subset [0,2\pi] \subset [0,2\pi]](/latexrender/pictures/cc29bce5d9bb88a0223ede1c35bc17d2.png)
. Calculando as integrais sobre os intervalos
![[0,\pi/6] , [\pi/6,5\pi/6] ,[5\pi/6 ,2\pi] [0,\pi/6] , [\pi/6,5\pi/6] ,[5\pi/6 ,2\pi]](/latexrender/pictures/81435ddd9846ef1d93390569c5804708.png)
e somando obterá o resultado . Em cada intervalo é possível ver qual curva está acima e abaixo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pessoa Estranha » Sex Jan 03, 2014 18:25
por Pessoa Estranha » Sex Jan 03, 2014 18:25
Olá!
Fiz como você disse, mas o meu resultado deu diferente. Olha, no wolframalpha deu
http://www.wolframalpha.com/input/?i=ar ... +0+to+2pi+ , mas no meu deu aproximadamente 10.12.
Penso que pode ser por conta da fórmula usada para calcular áreas de curvas em coordenadas polares (tem o 1/2 antes de cada integral). Será que estou certa?
Muito Obrigada pela ajuda!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sáb Jan 04, 2014 15:04
por e8group » Sáb Jan 04, 2014 15:04
Você tem razão ,pesquisei na internet e encontrei a fórmula que você mencionou . Achei interessante e quero estudar a dedução dá formula ,daí estarei habilitado p/ responder com mais certeza .Mas, aplicando a fórmula vc obteve o resultado que você citou ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pessoa Estranha » Sáb Jan 04, 2014 15:39
por Pessoa Estranha » Sáb Jan 04, 2014 15:39
Então, aplicando a fórmula eu cheguei numa expressão que equivale à aproximadamente 10.12, mas não sei se está certo; posso ter errado em alguma passagem de manipulação algébrica. Fiquei pensando que a área da curva em coordenadas polares seria igual à área da mesma curva, mas em coordenadas cartesianas e, por isso, acho que o meu resultado pode estar errado. Mas não tenho certeza. Na verdade, preciso estudar mais este assunto....
Obrigada!


-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Man Utd » Sáb Jan 04, 2014 20:00
por Man Utd » Sáb Jan 04, 2014 20:00
Eu acho que o correto seria:

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] ajudem urgente por favor nesse exercicio
por amanda s » Sáb Nov 16, 2013 17:27
- 1 Respostas
- 1919 Exibições
- Última mensagem por nakagumahissao

Dom Nov 17, 2013 10:04
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de Exercicio Urgente
por Mimizinha » Qua Mar 19, 2008 18:13
- 7 Respostas
- 18059 Exibições
- Última mensagem por Mimizinha

Qui Mar 20, 2008 12:58
Sistemas de Equações
-
- Estatística - Exercício Urgente
por Carlaipb » Qua Out 05, 2011 17:12
- 1 Respostas
- 2128 Exibições
- Última mensagem por Neperiano

Qua Out 19, 2011 18:52
Estatística
-
- Urgente:Exercício de probabilidade
por rudson01 » Qua Mai 22, 2013 00:18
- 1 Respostas
- 1696 Exibições
- Última mensagem por Rafael16

Qua Mai 22, 2013 11:07
Probabilidade
-
- Urgente:Exercício de probabilidade
por rudson01 » Qua Mai 22, 2013 00:44
- 1 Respostas
- 3483 Exibições
- Última mensagem por paulo testoni

Sex Jun 27, 2014 15:25
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . Na primeira volta , os ângulos cujo seno vale 1/2 são
. Na primeira volta , os ângulos cujo seno vale 1/2 são  e
e  . Tente esboçar as curvas . Pelo esboço das curvas você consegue concluir .
. Tente esboçar as curvas . Pelo esboço das curvas você consegue concluir .

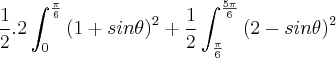 ?
?
 . Cada uma destas curvas podem ser descritas pelos subconjuntos do plano
. Cada uma destas curvas podem ser descritas pelos subconjuntos do plano  ,que são
,que são  e
e  . A interseção entre as duas curvas é descrita pelo conjunto ,
. A interseção entre as duas curvas é descrita pelo conjunto ,  .Logo ,
.Logo ,  sse
sse  e
e  sse
sse  e
e  ... Acredito que isto responde a sua dúvida
... Acredito que isto responde a sua dúvida![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) , e digitando
, e digitando![\subset [0,2\pi] \subset [0,2\pi]](/latexrender/pictures/cc29bce5d9bb88a0223ede1c35bc17d2.png) . Calculando as integrais sobre os intervalos
. Calculando as integrais sobre os intervalos ![[0,\pi/6] , [\pi/6,5\pi/6] ,[5\pi/6 ,2\pi] [0,\pi/6] , [\pi/6,5\pi/6] ,[5\pi/6 ,2\pi]](/latexrender/pictures/81435ddd9846ef1d93390569c5804708.png) e somando obterá o resultado . Em cada intervalo é possível ver qual curva está acima e abaixo .
e somando obterá o resultado . Em cada intervalo é possível ver qual curva está acima e abaixo .










 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.