Olá, pessoal!
Preciso de uma dica para encontrar a área da interseção das regiões limitadas pelas seguintes curvas:
http://www.wolframalpha.com/input/?i=rh ... 28theta%29
Obrigada!



 . Na primeira volta , os ângulos cujo seno vale 1/2 são
. Na primeira volta , os ângulos cujo seno vale 1/2 são  e
e  . Tente esboçar as curvas . Pelo esboço das curvas você consegue concluir .
. Tente esboçar as curvas . Pelo esboço das curvas você consegue concluir .

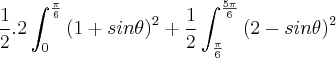 ?
?
 . Cada uma destas curvas podem ser descritas pelos subconjuntos do plano
. Cada uma destas curvas podem ser descritas pelos subconjuntos do plano  ,que são
,que são  e
e  . A interseção entre as duas curvas é descrita pelo conjunto ,
. A interseção entre as duas curvas é descrita pelo conjunto ,  .Logo ,
.Logo ,  sse
sse  e
e  sse
sse  e
e  ... Acredito que isto responde a sua dúvida
... Acredito que isto responde a sua dúvidaPessoa Estranha escreveu: Para calcular a interseção entre ambas, não consigo entender o que fazer.
![[0,2\pi] [0,2\pi]](/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) , e digitando
, e digitando![\subset [0,2\pi] \subset [0,2\pi]](/latexrender/pictures/cc29bce5d9bb88a0223ede1c35bc17d2.png) . Calculando as integrais sobre os intervalos
. Calculando as integrais sobre os intervalos ![[0,\pi/6] , [\pi/6,5\pi/6] ,[5\pi/6 ,2\pi] [0,\pi/6] , [\pi/6,5\pi/6] ,[5\pi/6 ,2\pi]](/latexrender/pictures/81435ddd9846ef1d93390569c5804708.png) e somando obterá o resultado . Em cada intervalo é possível ver qual curva está acima e abaixo .
e somando obterá o resultado . Em cada intervalo é possível ver qual curva está acima e abaixo .








Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes