 por pitagoras » Sáb Dez 28, 2013 17:01
por pitagoras » Sáb Dez 28, 2013 17:01
Pessoal alguém poderia me explicar porque a resposta é a b.
Considere a função
![f:[0, 5]\rightarrow R f:[0, 5]\rightarrow R](/latexrender/pictures/5b6d697b97198c3fa54ebc05dcbb2cde.png)
cujo gráfico está representado na figura a seguir:
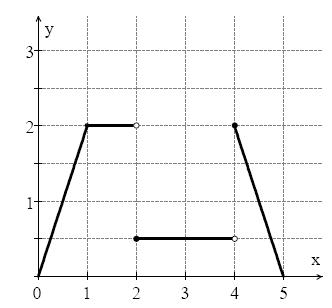
- 1.JPG (14.07 KiB) Exibido 1176 vezes
Assinale a alternativa que melhor representa o gráfico da função da
área delimitada pelo gráfico da função f e o eixo da abscissa, no intervalo
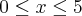
:
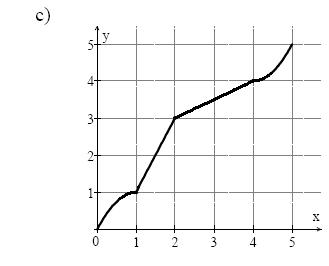
- 3.JPG (9.46 KiB) Exibido 1176 vezes
-
pitagoras
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Dez 28, 2013 11:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Normal
- Andamento: cursando
 por e8group » Ter Dez 31, 2013 14:31
por e8group » Ter Dez 31, 2013 14:31
Boa tarde . Através do gráfico fornecido , podemos obter a regra de associação da função
![f: [0,5] \mapsto \mathbb{R} f: [0,5] \mapsto \mathbb{R}](/latexrender/pictures/e8b1cb52eeb0ca24fd56ccc1a79e8f0d.png)
, a saber
![f(x) = \begin{cases} 2x ; x \in [0,1] \\ 2 ; x \in (1,2) \\ 1/2 ; x \in [2,4) \\ -2x + 10 ; x \in (4,5] \end{cases} f(x) = \begin{cases} 2x ; x \in [0,1] \\ 2 ; x \in (1,2) \\ 1/2 ; x \in [2,4) \\ -2x + 10 ; x \in (4,5] \end{cases}](/latexrender/pictures/a455e8b5b3d453c7fe9fb32267676c37.png)
.
Agora considere os quatros casos
![x \in [0,1] , x \in (1,2) , x \in [2,4) , x \in (4,5] x \in [0,1] , x \in (1,2) , x \in [2,4) , x \in (4,5]](/latexrender/pictures/278b1a153759caeaeec9821c655b2fc3.png)
.
No primeiro caso, a área da região delimitada pelo gráfico da função e o eixo x é a área do triângulo retângulo de base

e altura
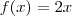
; no segundo caso , terá de calcular área de um retângulo de lados

e

; no terceiro deve calcular a área de um retângulo de lados

e
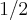
; no último caso , conforme no 1° , deve computar a área de um triângulo retângulo de mesma altura do primeiro ,porém bases distintas (em geral) que és 5 - x [/tex] .
Após finalizar tudo acima ,obterá uma regra de associação de uma função ,digamos

, definida do conjunto
![[0,5] [0,5]](/latexrender/pictures/be66a98c7ffb0b7cd18378674ce90c9c.png)
ao

.
Divirta-se!
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- FUNÇÃO DA ÁREA
por GabyRitter » Sáb Jun 20, 2009 21:14
- 1 Respostas
- 1382 Exibições
- Última mensagem por Cleyson007

Ter Jun 23, 2009 09:52
Funções
-
- Função e área
por estudante_2 » Qui Dez 16, 2010 14:41
- 1 Respostas
- 2207 Exibições
- Última mensagem por 0 kelvin

Qui Dez 16, 2010 21:32
Funções
-
- calcular a área da funçao
 por edilaine33 » Dom Dez 01, 2013 08:54
por edilaine33 » Dom Dez 01, 2013 08:54
- 1 Respostas
- 1709 Exibições
- Última mensagem por Pessoa Estranha

Dom Dez 01, 2013 10:13
Cálculo: Limites, Derivadas e Integrais
-
- calculo de área com função exponencial.
por Thiago 86 » Seg Set 16, 2013 12:34
- 6 Respostas
- 4590 Exibições
- Última mensagem por Thiago 86

Sex Set 20, 2013 16:57
Funções
-
- ÁREA DO TRIÂNGULO EM FUNÇÃO DOS LADOS
por Orlando Fagotti Neto » Qua Out 22, 2014 16:24
- 0 Respostas
- 1790 Exibições
- Última mensagem por Orlando Fagotti Neto

Qua Out 22, 2014 16:24
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f:[0, 5]\rightarrow R f:[0, 5]\rightarrow R](/latexrender/pictures/5b6d697b97198c3fa54ebc05dcbb2cde.png) cujo gráfico está representado na figura a seguir:
cujo gráfico está representado na figura a seguir: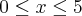 :
:
![f:[0, 5]\rightarrow R f:[0, 5]\rightarrow R](/latexrender/pictures/5b6d697b97198c3fa54ebc05dcbb2cde.png) cujo gráfico está representado na figura a seguir:
cujo gráfico está representado na figura a seguir: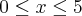 :
:
![f: [0,5] \mapsto \mathbb{R} f: [0,5] \mapsto \mathbb{R}](/latexrender/pictures/e8b1cb52eeb0ca24fd56ccc1a79e8f0d.png) , a saber
, a saber ![f(x) = \begin{cases} 2x ; x \in [0,1] \\ 2 ; x \in (1,2) \\ 1/2 ; x \in [2,4) \\ -2x + 10 ; x \in (4,5] \end{cases} f(x) = \begin{cases} 2x ; x \in [0,1] \\ 2 ; x \in (1,2) \\ 1/2 ; x \in [2,4) \\ -2x + 10 ; x \in (4,5] \end{cases}](/latexrender/pictures/a455e8b5b3d453c7fe9fb32267676c37.png) .
.![x \in [0,1] , x \in (1,2) , x \in [2,4) , x \in (4,5] x \in [0,1] , x \in (1,2) , x \in [2,4) , x \in (4,5]](/latexrender/pictures/278b1a153759caeaeec9821c655b2fc3.png) .
.  e altura
e altura 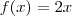 ; no segundo caso , terá de calcular área de um retângulo de lados
; no segundo caso , terá de calcular área de um retângulo de lados  e
e  ; no terceiro deve calcular a área de um retângulo de lados
; no terceiro deve calcular a área de um retângulo de lados  e
e 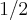 ; no último caso , conforme no 1° , deve computar a área de um triângulo retângulo de mesma altura do primeiro ,porém bases distintas (em geral) que és 5 - x [/tex] .
; no último caso , conforme no 1° , deve computar a área de um triângulo retângulo de mesma altura do primeiro ,porém bases distintas (em geral) que és 5 - x [/tex] .  , definida do conjunto
, definida do conjunto ![[0,5] [0,5]](/latexrender/pictures/be66a98c7ffb0b7cd18378674ce90c9c.png) ao
ao  .
.