 por Lana Brasil » Qua Dez 11, 2013 11:47
por Lana Brasil » Qua Dez 11, 2013 11:47
Bom dia.
Não consegui resolver essa questão, podem me ajudar por favor?
Dados f(g(x)) = x e g(x) = 2x-1, determine f(x)?
f(2x-1) = x mas não sei o que devo fazer depois porque foi dado g(x). Se fosse f(x) eu saberia continuar.
Agradeço a ajuda.
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 13:52
por e8group » Qua Dez 11, 2013 13:52
Boa tarde ,tente fazer este exercício seguindo as dicas abaixo
viewtopic.php?p=44689#p44689 . Tente concluir ,caso não consiga , diz até aonde conseguiu avançar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lana Brasil » Qua Dez 11, 2013 14:28
por Lana Brasil » Qua Dez 11, 2013 14:28
Obrigada pela ajuda. O exemplo que me deu é o que sei fazer. Nesse caso falta o f(x). Por isso não sei fazer.
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 14:40
por e8group » Qua Dez 11, 2013 14:40
Boa tarde . Note que
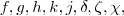
e etc. são só nomes sugestivos para a função .Aquelas dicas se adapta-a este caso . Se novamente não conseguir prosseguir ,post .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lana Brasil » Qua Dez 11, 2013 14:43
por Lana Brasil » Qua Dez 11, 2013 14:43
Eu realmente não consegui. Obrigada
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 16:00
por e8group » Qua Dez 11, 2013 16:00
Você tem razão ,agora que notei ,o que temos é
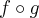
( e não

) e
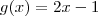
.
Observação .
Considere as funções
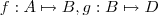
(com
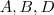
não vazios ). Admita

sobrejetiva , então

admite inversa à direita . Seja

inversa de

à direita .Pela hipótese
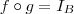
,onde
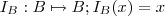
é a função identidade .Além disso , se

for também injetora e

for inversa à esquerda de

(ou seja,
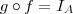
) ,então dizemos que

é invertível e

é sua inversa .
Em relação ao exercício , foi dado
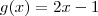
e

e queremos determinar

.Ora ,pela teoria acima

é sobrejetora e

sua inversa à direita . Agora se considerarmos

injetora e

sua inversa à esquerda ,chegaríamos a conclusão que
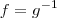
que é a função inversa de

. Agora basta determinar
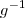
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lana Brasil » Qui Dez 12, 2013 09:44
por Lana Brasil » Qui Dez 12, 2013 09:44
santhiago escreveu:Você tem razão ,agora que notei ,o que temos é
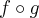
( e não

) e
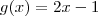
.
Observação .
Considere as funções
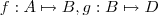
(com
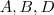
não vazios ). Admita

sobrejetiva , então

admite inversa à direita . Seja

inversa de

à direita .Pela hipótese
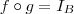
,onde
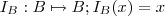
é a função identidade .Além disso , se

for também injetora e

for inversa à esquerda de

(ou seja,
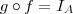
) ,então dizemos que

é invertível e

é sua inversa .
Em relação ao exercício , foi dado
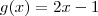
e

e queremos determinar

.Ora ,pela teoria acima

é sobrejetora e

sua inversa à direita . Agora se considerarmos

injetora e

sua inversa à esquerda ,chegaríamos a conclusão que
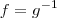
que é a função inversa de

. Agora basta determinar
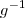
.
Obrigada pela sua boa vontade. A explicação teórica está difícil de entender para o pouco que sei de função, por enquanto. Mesmo assim muito obrigada. O que fiz foi isso: g(x)^-1 = (x+1)/2 então g((x+1)/2) = x e f(g(x)) = x então f(x) = (x+1)/2. Está correto??
-
Lana Brasil
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Dom Abr 07, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qui Dez 12, 2013 20:56
por e8group » Qui Dez 12, 2013 20:56
Lana Brasil escreveu:santhiago escreveu:Você tem razão ,agora que notei ,o que temos é
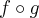
( e não

) e
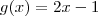
.
Observação .
Considere as funções
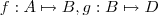
(com
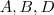
não vazios ). Admita

sobrejetiva , então

admite inversa à direita . Seja

inversa de

à direita .Pela hipótese
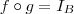
,onde
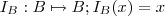
é a função identidade .Além disso , se

for também injetora e

for inversa à esquerda de

(ou seja,
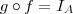
) ,então dizemos que

é invertível e

é sua inversa .
Em relação ao exercício , foi dado
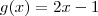
e

e queremos determinar

.Ora ,pela teoria acima

é sobrejetora e

sua inversa à direita . Agora se considerarmos

injetora e

sua inversa à esquerda ,chegaríamos a conclusão que
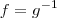
que é a função inversa de

. Agora basta determinar
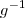
.
Obrigada pela sua boa vontade. A explicação teórica está difícil de entender para o pouco que sei de função, por enquanto. Mesmo assim muito obrigada. O que fiz foi isso: g(x)^-1 = (x+1)/2 então g((x+1)/2) = x e f(g(x)) = x então f(x) = (x+1)/2. Está correto??
Sim ,está correto .
OBS.: No youtube há um canal chamado Nerckie onde-se encontra videos aulas de matemática para ensino médio ,caso possui dúvidas fica a dica .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função composta]Achar o dominio de uma função composta
por lucasmath » Dom Abr 12, 2015 16:09
- 0 Respostas
- 2234 Exibições
- Última mensagem por lucasmath

Dom Abr 12, 2015 16:09
Funções
-
- [FUNÇÃO] NAO CONSIGO ENTENDER FUNÇÃO COMPOSTA!
por Gabriela AlmeidaS » Seg Mai 12, 2014 19:18
- 5 Respostas
- 5466 Exibições
- Última mensagem por Toussantt

Dom Jan 24, 2016 15:34
Funções
-
- Função composta
por scorpion » Sáb Out 25, 2008 11:09
- 2 Respostas
- 4205 Exibições
- Última mensagem por scorpion

Qua Out 29, 2008 14:26
Funções
-
- Função Composta
 por ginrj » Ter Jun 30, 2009 17:35
por ginrj » Ter Jun 30, 2009 17:35
- 4 Respostas
- 17049 Exibições
- Última mensagem por LuizAquino

Sáb Mar 03, 2012 14:34
Funções
-
- Função composta
 por matemalouco » Sáb Ago 15, 2009 20:43
por matemalouco » Sáb Ago 15, 2009 20:43
- 2 Respostas
- 3986 Exibições
- Última mensagem por Elcioschin

Seg Ago 17, 2009 10:26
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





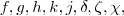 e etc. são só nomes sugestivos para a função .Aquelas dicas se adapta-a este caso . Se novamente não conseguir prosseguir ,post .
e etc. são só nomes sugestivos para a função .Aquelas dicas se adapta-a este caso . Se novamente não conseguir prosseguir ,post .

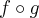 ( e não
( e não  ) e
) e 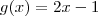 .
.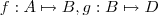 (com
(com 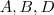 não vazios ). Admita
não vazios ). Admita  sobrejetiva , então
sobrejetiva , então  admite inversa à direita . Seja
admite inversa à direita . Seja  inversa de
inversa de  à direita .Pela hipótese
à direita .Pela hipótese 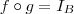 ,onde
,onde 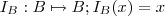 é a função identidade .Além disso , se
é a função identidade .Além disso , se  for também injetora e
for também injetora e  for inversa à esquerda de
for inversa à esquerda de  (ou seja,
(ou seja, 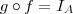 ) ,então dizemos que
) ,então dizemos que  é invertível e
é invertível e  é sua inversa .
é sua inversa .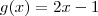 e
e  e queremos determinar
e queremos determinar  .Ora ,pela teoria acima
.Ora ,pela teoria acima  é sobrejetora e
é sobrejetora e  sua inversa à direita . Agora se considerarmos
sua inversa à direita . Agora se considerarmos  injetora e
injetora e  sua inversa à esquerda ,chegaríamos a conclusão que
sua inversa à esquerda ,chegaríamos a conclusão que 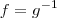 que é a função inversa de
que é a função inversa de  . Agora basta determinar
. Agora basta determinar 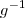 .
.
( e não
) e
.
(com
não vazios ). Admita
sobrejetiva , então
admite inversa à direita . Seja
inversa de
à direita .Pela hipótese
,onde
é a função identidade .Além disso , se
for também injetora e
for inversa à esquerda de
(ou seja,
) ,então dizemos que
é invertível e
é sua inversa .
e
e queremos determinar
.Ora ,pela teoria acima
é sobrejetora e
sua inversa à direita . Agora se considerarmos
injetora e
sua inversa à esquerda ,chegaríamos a conclusão que
que é a função inversa de
. Agora basta determinar
.

( e não
) e
.
(com
não vazios ). Admita
sobrejetiva , então
admite inversa à direita . Seja
inversa de
à direita .Pela hipótese
,onde
é a função identidade .Além disso , se
for também injetora e
for inversa à esquerda de
(ou seja,
) ,então dizemos que
é invertível e
é sua inversa .
e
e queremos determinar
.Ora ,pela teoria acima
é sobrejetora e
sua inversa à direita . Agora se considerarmos
injetora e
sua inversa à esquerda ,chegaríamos a conclusão que
que é a função inversa de
. Agora basta determinar
.
