 por dehcalegari » Seg Ago 26, 2013 18:42
por dehcalegari » Seg Ago 26, 2013 18:42
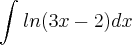
tentei usar u = ln(3x-2) e dv=dx, logo, du= dx/3x-2 e v=x...
Mas não cheguei a nada... ou melhor, até cheguei, mas um pouco ficou confuso... a derivada de ln(3x-2) está certa?
-
dehcalegari
- Usuário Parceiro

-
- Mensagens: 85
- Registrado em: Qui Abr 04, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por dehcalegari » Seg Ago 26, 2013 18:44
por dehcalegari » Seg Ago 26, 2013 18:44
ok, ja verifiquei que o du = 3/3x-2 dx
e agora?
-
dehcalegari
- Usuário Parceiro

-
- Mensagens: 85
- Registrado em: Qui Abr 04, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por Russman » Seg Ago 26, 2013 18:48
por Russman » Seg Ago 26, 2013 18:48
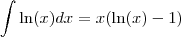
Assim, se você tomar
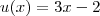
, então
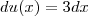
e portanto
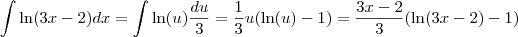
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por dehcalegari » Seg Ago 26, 2013 18:54
por dehcalegari » Seg Ago 26, 2013 18:54
a resposta tem que dar
x ln(3x-2) - x - 2/3 ln(3x-2) + C
-
dehcalegari
- Usuário Parceiro

-
- Mensagens: 85
- Registrado em: Qui Abr 04, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por dehcalegari » Seg Ago 26, 2013 18:57
por dehcalegari » Seg Ago 26, 2013 18:57
Não teria que fazer u(x) = ln(3x-2), com du = 3/3x-2 dx e ... dv=dx, com v=x ???
Porque ai eu cheguei a:

Só que parei por aqui dai...
-
dehcalegari
- Usuário Parceiro

-
- Mensagens: 85
- Registrado em: Qui Abr 04, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por Russman » Seg Ago 26, 2013 19:26
por Russman » Seg Ago 26, 2013 19:26
dehcalegari escreveu:a resposta tem que dar
x ln(3x-2) - x - 2/3 ln(3x-2) + C
Mas a resposta dá isso. É só simplificar.
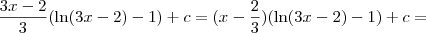
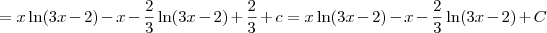
dehcalegari escreveu:Não teria que fazer u(x) = ln(3x-2), com du = 3/3x-2 dx e ... dv=dx, com v=x ???
Porque ai eu cheguei a:
Você não precisa usar esse tratamento pois não há um produto de funções no integrando. Note que fazê-lo seria redundante, já que para resolver a integral que você chegou seria necessário utilizar integração por substituição que é o método que eu te mostrei.
Entende?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por dehcalegari » Seg Ago 26, 2013 21:32
por dehcalegari » Seg Ago 26, 2013 21:32
Entendi. E o 2/3 ele considerou como C. Fechou. Valeu.
-
dehcalegari
- Usuário Parceiro

-
- Mensagens: 85
- Registrado em: Qui Abr 04, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por Russman » Seg Ago 26, 2013 21:43
por Russman » Seg Ago 26, 2013 21:43
O 2/3 é consumido pela constante, já que ela é arbitrária.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por dehcalegari » Ter Ago 27, 2013 10:12
por dehcalegari » Ter Ago 27, 2013 10:12
-
dehcalegari
- Usuário Parceiro

-
- Mensagens: 85
- Registrado em: Qui Abr 04, 2013 09:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4623 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4590 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4348 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2848 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2874 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

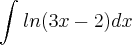






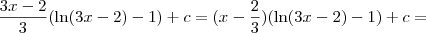
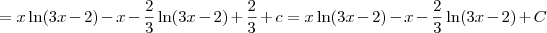






 , avisa que eu resolvo.
, avisa que eu resolvo.

