Olá pessoal! Obrigada por terem respondido.
Estou estudando através de um livro de cálculo, e, nele, realmente está escrito que devemos aplicar a regra da cadeia em derivadas de funções compostas, porém, há uma parte que diz o seguinte:
"Sendo
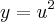
com
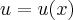
derivável, resulta
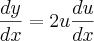
. Por outro lado,
![y={u}^{2}\Rightarrow \frac{dy}{du}=\frac{d}{du}[{u}^{2}]=2u y={u}^{2}\Rightarrow \frac{dy}{du}=\frac{d}{du}[{u}^{2}]=2u](/latexrender/pictures/f54952981d1a69e57a393a27c0954b0f.png)
. Assim,
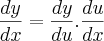
onde
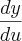
deve ser calculado em
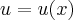
. Provaremos mais adiante que esta regra, conhecida como regra da cadeia, é válida sempre que
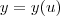
e
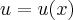
forem deriváveis".
Na última frase, realmente está claro que trata-se de funções compostas, mas no início eu entendi que a regra da cadeia poderia ser usada em casos como:
"Seja

com
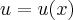
função derivável. Verifique que
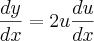
".
Este é, na verdade, bastante semelhante com o exercício que enviei aqui. Então pensei que pudesse ser assim, mas pelo visto fiz uma interpretação errada. O livro só confundiu-me!
Valeu pessoal! Obrigada pela ajuda!
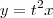 , onde
, onde 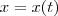 é uma função derivável. Calcule
é uma função derivável. Calcule 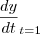 , supondo
, supondo 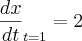 e x=3 para t=1.
e x=3 para t=1.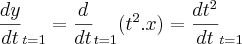
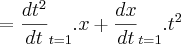
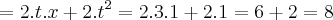 .
.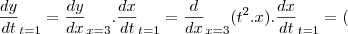
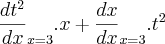 )
)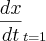 =6
=6


 é função real de uma variável real assim como a função
é função real de uma variável real assim como a função 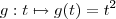 também o é .Como ambas funções possuem regras de associações dependentes da mesma variável
também o é .Como ambas funções possuem regras de associações dependentes da mesma variável  .Logo o produto destas funções fornecerá uma nova função cuja regra de associação(também só dependendo de
.Logo o produto destas funções fornecerá uma nova função cuja regra de associação(também só dependendo de 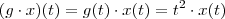 . Na minha opinião o resultado que temos que usar para derivar esta função é a regra do produto e não a regra da cadeia . Espero que ajude .
. Na minha opinião o resultado que temos que usar para derivar esta função é a regra do produto e não a regra da cadeia . Espero que ajude .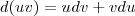
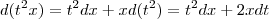 e
e 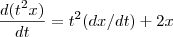 . Desse modo, para
. Desse modo, para  , temos
, temos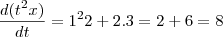 .
. com
com 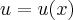 derivável, resulta
derivável, resulta 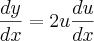 . Por outro lado,
. Por outro lado, ![y={u}^{2}\Rightarrow \frac{dy}{du}=\frac{d}{du}[{u}^{2}]=2u y={u}^{2}\Rightarrow \frac{dy}{du}=\frac{d}{du}[{u}^{2}]=2u](/latexrender/pictures/f54952981d1a69e57a393a27c0954b0f.png) . Assim,
. Assim, 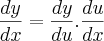 onde
onde 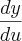 deve ser calculado em
deve ser calculado em 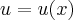 . Provaremos mais adiante que esta regra, conhecida como regra da cadeia, é válida sempre que
. Provaremos mais adiante que esta regra, conhecida como regra da cadeia, é válida sempre que 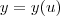 e
e ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)