 por anneliesero » Seg Jul 22, 2013 12:09
por anneliesero » Seg Jul 22, 2013 12:09
Olá, pessoal

nesses exercícios aqui não estão conferindo com o gabarito. Alguém poderia por favor identificar onde está o erro? Não consegui terminar sendo que não exite raiz cúbica exata desses números...
Simplifique as raízes cúbicas:
![\sqrt[3]{500}=\sqrt[3]{5.100}=\sqrt[3]{5}.\sqrt[3]{100} \sqrt[3]{500}=\sqrt[3]{5.100}=\sqrt[3]{5}.\sqrt[3]{100}](/latexrender/pictures/61cf7b07d963be9d06b79cc65f7f86ee.png)
![\sqrt[3]{320}=\sqrt[3]{4.80}=\sqrt[3]{4}.\sqrt[3]{80} \sqrt[3]{320}=\sqrt[3]{4.80}=\sqrt[3]{4}.\sqrt[3]{80}](/latexrender/pictures/bde66e5ad42a7bd74aced09d9293bdc8.png)
![\sqrt[3]{-81}=\sqrt[3]{9.-9}=\sqrt[3]{3.-3}.\sqrt[3]{3.3}=-3\sqrt[3]{3} \sqrt[3]{-81}=\sqrt[3]{9.-9}=\sqrt[3]{3.-3}.\sqrt[3]{3.3}=-3\sqrt[3]{3}](/latexrender/pictures/26a12544744027db10ba762cd20432b7.png)
Os resultados são respectivamente:
![5\sqrt[3]{3} 5\sqrt[3]{3}](/latexrender/pictures/58a6fc46f0845e880cd6aef6fcb091ab.png)
,
![4\sqrt[3]{5} 4\sqrt[3]{5}](/latexrender/pictures/34b5e71191c992181601e356a60830e4.png)
,
![-3\sqrt[3]{3} -3\sqrt[3]{3}](/latexrender/pictures/a91e8466260d76b3d991bbd8374b1ad0.png)
.
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por temujin » Seg Jul 22, 2013 15:01
por temujin » Seg Jul 22, 2013 15:01
Olá.
Perceba o seguinte: Uma raiz enésima qualquer pode sempre ser escrita como
![\sqrt[n]a = a^{1/n} \sqrt[n]a = a^{1/n}](/latexrender/pictures/382b36e65d9fcaf8b11080773a78d1f9.png)
. Portanto, se vc elevar este número a n, vc terá
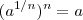
No seu caso vc tem uma raiz cúbica. Então, como vc pode "tirar" um número de dentro desta raiz? Expressando ele como alguma potência de 3. Vamos pegar suas questões:
![\sqrt[3]{500} =\sqrt[3]{5^3.4} = 5\sqrt[3]{4} \sqrt[3]{500} =\sqrt[3]{5^3.4} = 5\sqrt[3]{4}](/latexrender/pictures/517f8f1a54af25be5f722c0be52a7ab4.png)
(confira o gabarito pra ver se é raiz de 3 ou 4)
![\sqrt[3]{420} =\sqrt[3]{4^3.5} = 4\sqrt[3]{5} \sqrt[3]{420} =\sqrt[3]{4^3.5} = 4\sqrt[3]{5}](/latexrender/pictures/27acb069a91dc6681d1aedb01642c964.png)
Tente concluir o terceiro.
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Radiciação
por thadeu » Qua Nov 18, 2009 16:32
- 1 Respostas
- 1704 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 18:01
Álgebra Elementar
-
- Radiciaçao
por guillcn » Ter Abr 12, 2011 17:17
- 2 Respostas
- 2225 Exibições
- Última mensagem por guillcn

Ter Abr 12, 2011 18:05
Álgebra Elementar
-
- Radiciação
por marianne86 » Sex Set 02, 2011 02:05
- 1 Respostas
- 1171 Exibições
- Última mensagem por LuizAquino

Sex Set 02, 2011 11:16
Álgebra Elementar
-
- Radiciação
por TAE » Qua Mai 16, 2012 18:03
- 8 Respostas
- 4308 Exibições
- Última mensagem por DanielFerreira

Ter Mai 22, 2012 23:00
Álgebra Elementar
-
- Radiciação
por misaelbarreto » Sáb Out 24, 2015 21:23
- 1 Respostas
- 1226 Exibições
- Última mensagem por Cleyson007

Seg Out 26, 2015 17:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\sqrt[3]{500}=\sqrt[3]{5.100}=\sqrt[3]{5}.\sqrt[3]{100} \sqrt[3]{500}=\sqrt[3]{5.100}=\sqrt[3]{5}.\sqrt[3]{100}](/latexrender/pictures/61cf7b07d963be9d06b79cc65f7f86ee.png)
![\sqrt[3]{320}=\sqrt[3]{4.80}=\sqrt[3]{4}.\sqrt[3]{80} \sqrt[3]{320}=\sqrt[3]{4.80}=\sqrt[3]{4}.\sqrt[3]{80}](/latexrender/pictures/bde66e5ad42a7bd74aced09d9293bdc8.png)
![\sqrt[3]{-81}=\sqrt[3]{9.-9}=\sqrt[3]{3.-3}.\sqrt[3]{3.3}=-3\sqrt[3]{3} \sqrt[3]{-81}=\sqrt[3]{9.-9}=\sqrt[3]{3.-3}.\sqrt[3]{3.3}=-3\sqrt[3]{3}](/latexrender/pictures/26a12544744027db10ba762cd20432b7.png)
![5\sqrt[3]{3} 5\sqrt[3]{3}](/latexrender/pictures/58a6fc46f0845e880cd6aef6fcb091ab.png) ,
, ![4\sqrt[3]{5} 4\sqrt[3]{5}](/latexrender/pictures/34b5e71191c992181601e356a60830e4.png) ,
, ![-3\sqrt[3]{3} -3\sqrt[3]{3}](/latexrender/pictures/a91e8466260d76b3d991bbd8374b1ad0.png) .
.

![\sqrt[n]a = a^{1/n} \sqrt[n]a = a^{1/n}](/latexrender/pictures/382b36e65d9fcaf8b11080773a78d1f9.png) . Portanto, se vc elevar este número a n, vc terá
. Portanto, se vc elevar este número a n, vc terá 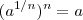
![\sqrt[3]{500} =\sqrt[3]{5^3.4} = 5\sqrt[3]{4} \sqrt[3]{500} =\sqrt[3]{5^3.4} = 5\sqrt[3]{4}](/latexrender/pictures/517f8f1a54af25be5f722c0be52a7ab4.png) (confira o gabarito pra ver se é raiz de 3 ou 4)
(confira o gabarito pra ver se é raiz de 3 ou 4)![\sqrt[3]{420} =\sqrt[3]{4^3.5} = 4\sqrt[3]{5} \sqrt[3]{420} =\sqrt[3]{4^3.5} = 4\sqrt[3]{5}](/latexrender/pictures/27acb069a91dc6681d1aedb01642c964.png)
