Não sei se esta correto isso mas, vamos lá:
É dado o exercicio:
Ache a área da superfice gerada pela revolução da curva em torno da eixo-y.
 e
e  ,
, 
Resolvendo:
á area será dada por (Aqui eu não detalhei os calculos que eu fiz, apenas resumi para ver se esta certo, se tem como resolver a integral que eu cheguei)
![\int_{0}^{\frac{\pi}{2}}2\pi{e}^{t}sen(t)\sqrt[]{2{e}^{2t}}dt=2\pi\sqrt[]{2}\int_{0}^{\frac{\pi}{2}}{e}^{2t}sen(t)dt \int_{0}^{\frac{\pi}{2}}2\pi{e}^{t}sen(t)\sqrt[]{2{e}^{2t}}dt=2\pi\sqrt[]{2}\int_{0}^{\frac{\pi}{2}}{e}^{2t}sen(t)dt](/latexrender/pictures/8a0eb4fd2ac7b851af34052339bbe60c.png)
e ai que esta o problema, como que resolvo isso
 ??????
??????já tentei por partes mas não consegui chegar em nada.
obrigado pela ajuda!!


 .Esta integral pode ser resolvida aplicando duas vezes a técnica de integração por partes . Integrar tal expressão torna-se achar a solução da equação para
.Esta integral pode ser resolvida aplicando duas vezes a técnica de integração por partes . Integrar tal expressão torna-se achar a solução da equação para 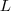 (Verifique ! ) . Tente concluir .
(Verifique ! ) . Tente concluir .
 e
e  , logo
, logo  e
e 
 =
= 

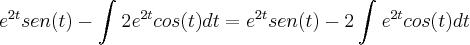 e mesmo substiuindo isso la na ultima integral que é multiplicada por 2, não resolverá muita coisa...
e mesmo substiuindo isso la na ultima integral que é multiplicada por 2, não resolverá muita coisa... .
. .
.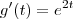 e
e  ; obtemos
; obtemos  e
e  .Assim , o integrando
.Assim , o integrando  pode ser reescrito como
pode ser reescrito como  .Daí ,
.Daí ,  .
. .
.  . E portanto ,
. E portanto , .
.  .
.  .
.  em evidência segue o resultado fornecido pelo Wolframalpha .As resposta são equivalentes .
em evidência segue o resultado fornecido pelo Wolframalpha .As resposta são equivalentes .
 .
.
 :
: