 por fabriel » Seg Mai 06, 2013 01:26
por fabriel » Seg Mai 06, 2013 01:26
E ai Pessoal, cheguei em uma expressão meio complicada de se resolver.
Não sei se esta correto isso mas, vamos lá:
É dado o exercicio:
Ache a área da superfice gerada pela revolução da curva em torno da eixo-y.

e

,

Resolvendo:
á area será dada por (Aqui eu não detalhei os calculos que eu fiz, apenas resumi para ver se esta certo, se tem como resolver a integral que eu cheguei)
![\int_{0}^{\frac{\pi}{2}}2\pi{e}^{t}sen(t)\sqrt[]{2{e}^{2t}}dt=2\pi\sqrt[]{2}\int_{0}^{\frac{\pi}{2}}{e}^{2t}sen(t)dt \int_{0}^{\frac{\pi}{2}}2\pi{e}^{t}sen(t)\sqrt[]{2{e}^{2t}}dt=2\pi\sqrt[]{2}\int_{0}^{\frac{\pi}{2}}{e}^{2t}sen(t)dt](/latexrender/pictures/8a0eb4fd2ac7b851af34052339bbe60c.png)
e ai que esta o problema, como que resolvo isso

??????
já tentei por partes mas não consegui chegar em nada.
obrigado pela ajuda!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Seg Mai 06, 2013 02:40
por e8group » Seg Mai 06, 2013 02:40
Tome

.Esta integral pode ser resolvida aplicando duas vezes a técnica de integração por partes . Integrar tal expressão torna-se achar a solução da equação para
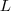
(Verifique ! ) . Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Seg Mai 06, 2013 14:05
por fabriel » Seg Mai 06, 2013 14:05
Eu já tentei fazer desse jeito , mas não consegui. Veja
Temos que resolver essa Integral

Então chamando

e

, logo

e

Então fazendo a integração por partes

=

Agora temos outro problema, essa integral:

Mesmo se eu fizer agora de novo, não ira resolver muita coisa.
chegarei na seguinte expressão:
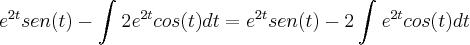
e mesmo substiuindo isso la na ultima integral que é multiplicada por 2, não resolverá muita coisa...
E isso não irá resolver nada..
Então você chegou num resultado??
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Seg Mai 06, 2013 20:56
por e8group » Seg Mai 06, 2013 20:56
Considere :

.
Por integração por partes ,segue-se que :

.
Lembrando que
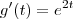
e

; obtemos

e

.Assim , o integrando

pode ser reescrito como

.Daí ,

.
E novamente por int. por partes ,temos :

.
Logo ,

. E portanto ,

.
Resolvendo e equação para
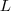
, resulta :

.

.
Só para confirmar a resposta :
http://www.wolframalpha.com/input/?i=%5 ... %28t%29+dtAgora tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por fabriel » Ter Mai 07, 2013 03:05
por fabriel » Ter Mai 07, 2013 03:05
Que beleza heim, Obrigado ai.
Hoje de noite eu estava na universidade e acabei resolvendo ela tbm!!
Só não entendi a resposta que você me passo? Parece que lá a resposta foi multiplicada por -1...
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por e8group » Ter Mai 07, 2013 21:12
por e8group » Ter Mai 07, 2013 21:12
fabriel escreveu:Que beleza heim, Obrigado ai.
Hoje de noite eu estava na universidade e acabei resolvendo ela tbm!!
Só não entendi a resposta que você me passo? Parece que lá a resposta foi multiplicada por -1...
De nada . Deixando

em evidência segue o resultado fornecido pelo Wolframalpha .As resposta são equivalentes .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Integração por partes
por bencz » Sex Abr 22, 2016 16:18
- 1 Respostas
- 3697 Exibições
- Última mensagem por nakagumahissao

Sáb Abr 23, 2016 23:33
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por Partes] Integral indefinida...
por luiz_henriquear » Qui Dez 22, 2011 17:40
- 1 Respostas
- 3717 Exibições
- Última mensagem por LuizAquino

Qui Dez 22, 2011 21:58
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por Partes] Integral indefinida...
por luiz_henriquear » Sáb Dez 31, 2011 14:35
- 2 Respostas
- 1968 Exibições
- Última mensagem por luiz_henriquear

Sáb Dez 31, 2011 15:08
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Duvida na integração Por partes
por fabriel » Sáb Out 06, 2012 18:56
- 1 Respostas
- 1588 Exibições
- Última mensagem por MarceloFantini

Sáb Out 06, 2012 19:17
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Integral com integração por partes
por karenfreitas » Qui Jun 30, 2016 18:16
- 2 Respostas
- 5062 Exibições
- Última mensagem por karenfreitas

Seg Jul 18, 2016 18:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  ,
, 
![\int_{0}^{\frac{\pi}{2}}2\pi{e}^{t}sen(t)\sqrt[]{2{e}^{2t}}dt=2\pi\sqrt[]{2}\int_{0}^{\frac{\pi}{2}}{e}^{2t}sen(t)dt \int_{0}^{\frac{\pi}{2}}2\pi{e}^{t}sen(t)\sqrt[]{2{e}^{2t}}dt=2\pi\sqrt[]{2}\int_{0}^{\frac{\pi}{2}}{e}^{2t}sen(t)dt](/latexrender/pictures/8a0eb4fd2ac7b851af34052339bbe60c.png)
 ??????
??????

 .Esta integral pode ser resolvida aplicando duas vezes a técnica de integração por partes . Integrar tal expressão torna-se achar a solução da equação para
.Esta integral pode ser resolvida aplicando duas vezes a técnica de integração por partes . Integrar tal expressão torna-se achar a solução da equação para 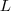 (Verifique ! ) . Tente concluir .
(Verifique ! ) . Tente concluir .
 e
e  , logo
, logo  e
e 
 =
= 

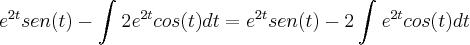 e mesmo substiuindo isso la na ultima integral que é multiplicada por 2, não resolverá muita coisa...
e mesmo substiuindo isso la na ultima integral que é multiplicada por 2, não resolverá muita coisa... .
. .
.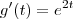 e
e  ; obtemos
; obtemos  e
e  .Assim , o integrando
.Assim , o integrando  pode ser reescrito como
pode ser reescrito como  .Daí ,
.Daí ,  .
. .
.  . E portanto ,
. E portanto , .
.  .
.  .
.  em evidência segue o resultado fornecido pelo Wolframalpha .As resposta são equivalentes .
em evidência segue o resultado fornecido pelo Wolframalpha .As resposta são equivalentes .