 por Jhennyfer » Sex Abr 12, 2013 23:13
por Jhennyfer » Sex Abr 12, 2013 23:13
Um polígono regular possui a partir de cada um de seus vertices tantas diagonais quantas são as diagonais de um hexagono. Cada angulo interno desse poligono mede em graus:
Boom, pelo que eu entendi...
1º) número de diagonais do poligono hexagono
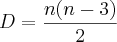
===>
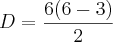
===>
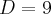
2º) Número de diagonais do hexágono é igual ao número de vertices do poligono, no caso 9...
então...
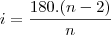
====>
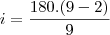
===>
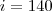
Porém, no gabarito a alternativa 140º está incorreta, e o resultado é 150º e eu não consigo chegar nesse resultado!
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sáb Abr 13, 2013 00:07
por e8group » Sáb Abr 13, 2013 00:07
Suponha que este polígono tenha

lados , observe que este polígono terá

vertices também ,certo ? Agora vamos ler o texto atentamente
" Um polígono regular possui a partir de cada um de seus vertices tantas diagonais quantas são as diagonais de um hexagono ... " .
Traduzindo : A parti de cada vértice há
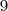
diagonais (valor este que você achou) ;mas por outro lado ,este polígono possui em cada vértice

diagonais ,concorda ? (Verifique o número de diagonais a parti de cada vértice do quadrilátero , pentágono , hexágono , e etc .)
Em resumo temos
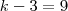
,donde obtemos

.
Consegue concluir ??
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhennyfer » Seg Abr 22, 2013 12:19
por Jhennyfer » Seg Abr 22, 2013 12:19
agora deu certo, obrigado!
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com exercicio!!!
por tuany » Seg Mar 24, 2008 15:34
- 3 Respostas
- 4128 Exibições
- Última mensagem por tuany

Ter Mar 25, 2008 16:50
Funções
-
- Ajuda com exercicio!!!
por karol_agnelli » Qua Mar 26, 2008 19:40
- 6 Respostas
- 7293 Exibições
- Última mensagem por Cleyson007

Qua Jun 10, 2009 15:23
Tópicos sem Interação (leia as regras)
-
- ajuda com o exercicio
por Mimizinha » Seg Mar 31, 2008 18:19
- 2 Respostas
- 3499 Exibições
- Última mensagem por Mimizinha

Ter Abr 01, 2008 10:24
Geometria Plana
-
- Ajuda em Exercício.
 por Levi23 » Dom Set 28, 2008 02:01
por Levi23 » Dom Set 28, 2008 02:01
- 12 Respostas
- 8861 Exibições
- Última mensagem por admin

Sáb Out 04, 2008 13:51
Trigonometria
-
- ajuda em exercicio
por anabela » Qua Nov 25, 2009 15:31
- 2 Respostas
- 3138 Exibições
- Última mensagem por anabatista

Ter Abr 09, 2013 00:10
Estatística para Licenciatura I
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
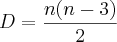 ===>
===> 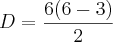 ===>
===> 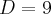
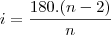 ====>
====> 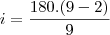 ===>
===> 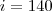


 lados , observe que este polígono terá
lados , observe que este polígono terá 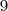 diagonais (valor este que você achou) ;mas por outro lado ,este polígono possui em cada vértice
diagonais (valor este que você achou) ;mas por outro lado ,este polígono possui em cada vértice  diagonais ,concorda ? (Verifique o número de diagonais a parti de cada vértice do quadrilátero , pentágono , hexágono , e etc .)
diagonais ,concorda ? (Verifique o número de diagonais a parti de cada vértice do quadrilátero , pentágono , hexágono , e etc .)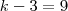 ,donde obtemos
,donde obtemos  .
.