Ajuda no exercício

[Jhennyfer]

Um polígono regular possui a partir de cada um de seus vertices tantas diagonais quantas são as diagonais de um hexagono. Cada angulo interno desse poligono mede em graus:

Boom, pelo que eu entendi...
1º) número de diagonais do poligono hexagono

===> ===>

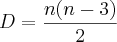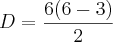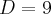
2º) Número de diagonais do hexágono é igual ao número de vertices do poligono, no caso 9...
então...

====> ===>

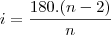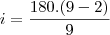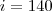
Porém, no gabarito a alternativa 140º está incorreta, e o resultado é 150º e eu não consigo chegar nesse resultado!

[e8group]

Suponha que este polígono tenha lados , observe que este polígono terá 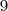vertices também ,certo ? Agora vamos ler o texto atentamente

" Um polígono regular possui a partir de cada um de seus vertices tantas diagonais quantas são as diagonais de um hexagono ... " .

Traduzindo : A parti de cada vértice há diagonais (valor este que você achou) ;mas por outro lado ,este polígono possui em cada vértice diagonais ,concorda ? (Verifique o número de diagonais a parti de cada vértice do quadrilátero , pentágono , hexágono , e etc .)

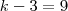Em resumo temos ,donde obtemos .

Consegue concluir ??

[Jhennyfer]

agora deu certo, obrigado!