
Não consegui fazer esse exercício. Como uso o valor do ângulo para chegar no resultado?
Tentei usando que é um quadrilátero então são dois a dois iguais, está errado?
A resposta é "raíz de 7"
Obrigada pela ajuda.



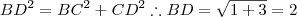 .Por relações trigonométricas é fácil verificar que o segmento
.Por relações trigonométricas é fácil verificar que o segmento 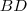 é perpendicular a
é perpendicular a 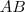 e portanto o triângulo
e portanto o triângulo 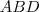 também é retângulo .Assim ,novamente pelo teorema de Pitágoras ,ele nos fornece que
também é retângulo .Assim ,novamente pelo teorema de Pitágoras ,ele nos fornece que 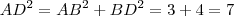 ;logo concluímos
;logo concluímos  .
.
santhiago escreveu:Observe o triângulo retânguloBCD ,por Pitágoras ,segue.Por relações trigonométricas é fácil verificar que o segmento
é perpendicular a
e portanto o triângulo
também é retângulo .Assim ,novamente pelo teorema de Pitágoras ,ele nos fornece que
;logo concluímos
.

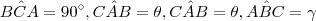 com
com  e
e  ângulos agudos (menores que 90°) tais que
ângulos agudos (menores que 90°) tais que 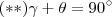 .
.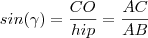
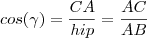
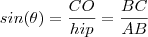
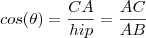
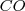 : Cateto oposto (em relação ao ângulo)
: Cateto oposto (em relação ao ângulo)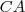 : Cateto adjacente (em relação ao ângulo)
: Cateto adjacente (em relação ao ângulo) 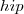 : Hipotenusa (oposto ao ângulo reto)
: Hipotenusa (oposto ao ângulo reto)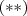 (Veja lá) e que um deles é reto (
(Veja lá) e que um deles é reto (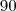 .) .Para esta questão,se mostrarmos que o ângulo
.) .Para esta questão,se mostrarmos que o ângulo 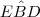 vale
vale 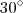 poderemos concluir que
poderemos concluir que 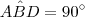 uma vez que
uma vez que 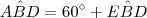 .Bom ,é isto que vamos fazer .Veja que
.Bom ,é isto que vamos fazer .Veja que 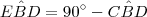 (Por quê ?) e que
(Por quê ?) e que 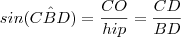 .
.  e no post anterior calculamos
e no post anterior calculamos 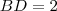 .Então ,
.Então ,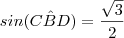 e portanto ,
e portanto ,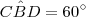 .Lembrando que
.Lembrando que 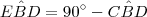 ,resulta
,resulta 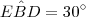 .Assim ,demonstramos que o ângulo
.Assim ,demonstramos que o ângulo 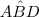 é reto.Além disso ,
é reto.Além disso ,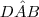 e
e 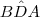 são ângulos agudos e
são ângulos agudos e 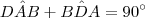 .Logo ,segue o resultado .
.Logo ,segue o resultado .
santhiago escreveu:Definimos as relações trigonométricas (seno e cosseno) em um triângulo ABC que é retângulo em C da seguinte forma :
Considere :com
e
ângulos agudos (menores que 90°) tais que
.
Temos :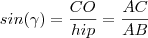
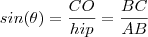
Onde :: Cateto oposto (em relação ao ângulo)
: Cateto adjacente (em relação ao ângulo)
: Hipotenusa (oposto ao ângulo reto)
OBS.: Uma vez que você não aprendeu ainda sobre seno e cosseno ,não vou falar sobre tangente .Além da função chamada tangente ,há outras três que são cotangente ,secante e cossecante .Não se preocupe ,todas elas estão relacionadas com seno e cosseno .
Para mostramos que o triângulo ABD é retângulo .Deveremos mostrar que dois de seus ângulos são agudos e satisfaçam(Veja lá) e que um deles é reto (
.) .Para esta questão,se mostrarmos que o ângulo
vale
poderemos concluir que
uma vez que
.Bom ,é isto que vamos fazer .Veja que
(Por quê ?) e que
.
Como foi dado quee no post anterior calculamos
.Então ,
e portanto ,
.Lembrando que
,resulta
.Assim ,demonstramos que o ângulo
é reto.Além disso ,
e
são ângulos agudos e
.Logo ,segue o resultado .

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

