 por samysoares » Seg Mar 04, 2013 13:38
por samysoares » Seg Mar 04, 2013 13:38
f(x) = 2xcosxtgx
f'(x)=?
não consigo resolver essa questão, o meu resultado não bate com o gabarito de jeito nenhum. Por favor, se puder resolver passo a passo.
-
samysoares
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 08, 2013 12:42
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por marinalcd » Seg Mar 04, 2013 14:26
por marinalcd » Seg Mar 04, 2013 14:26
Consideremos uma função do tipo a.b.c
Para derivarmos esse produto, utilizaremos a regra do produto, ou seja:
f ' (x) = a'.b.c + a.b'.c + a.b.c'
Então:
f(x) = 2x.cosx.tgx
f ' (x) = (2x)'.cos xtg x + 2x(cos x)'.tg x + 2x.cos x.(tg x)'
f ' (x) = 2cos x.tg x + 2x (-sen x).tg x+ 2x.cos x.sec² x
f ' (x) = 2.cos x .tg x + -2x.sen x. tg x + 2x. cos x. sec² x
Espero ter ajudado!!!
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por samysoares » Qua Mar 06, 2013 12:46
por samysoares » Qua Mar 06, 2013 12:46
Infelizmente o gabarito não parou por aí, o resultado está simplificado, Mas obrigada, acho que consigo simplificar!
-
samysoares
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 08, 2013 12:42
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qua Mar 06, 2013 13:51
por e8group » Qua Mar 06, 2013 13:51
Boa tarde .Há outra forma também, simplificando

,ficando apenas com

.
Visto que
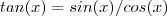
,então
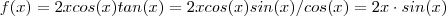
.
Pela regra do produto ,
![f'(x) = [2x \cdot sin(x)]' = (2x)' \cdot sin(x) + 2x \cdot( sin(x))' f'(x) = [2x \cdot sin(x)]' = (2x)' \cdot sin(x) + 2x \cdot( sin(x))'](/latexrender/pictures/a1116961b541338a2bdfff89cd801ef5.png)
;tente concluir ,talvez o desenvlovimento acima está no formato do seu gabarito ,se não ,post !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por marinalcd » Sex Mar 08, 2013 15:29
por marinalcd » Sex Mar 08, 2013 15:29
Poste o gabarito para a gente!
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [derivada de funçoes diferenciais]
por lucasdemirand » Qua Ago 07, 2013 00:34
- 1 Respostas
- 1500 Exibições
- Última mensagem por Russman

Qua Ago 07, 2013 15:46
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] derivada de funções trigonometricas
por beel » Qua Set 21, 2011 13:09
- 3 Respostas
- 2634 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:07
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de divisão de funções trigonométricas
por Fernandobertolaccini » Ter Jul 08, 2014 17:37
- 1 Respostas
- 1364 Exibições
- Última mensagem por e8group

Ter Jul 08, 2014 17:45
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada Parcial - Teorema das Funções Implícitas]
por raimundoocjr » Qua Nov 06, 2013 21:16
- 0 Respostas
- 1187 Exibições
- Última mensagem por raimundoocjr

Qua Nov 06, 2013 21:16
Cálculo: Limites, Derivadas e Integrais
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3429 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 ,ficando apenas com
,ficando apenas com  .
. 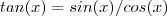 ,então
,então 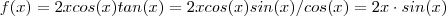 .
.![f'(x) = [2x \cdot sin(x)]' = (2x)' \cdot sin(x) + 2x \cdot( sin(x))' f'(x) = [2x \cdot sin(x)]' = (2x)' \cdot sin(x) + 2x \cdot( sin(x))'](/latexrender/pictures/a1116961b541338a2bdfff89cd801ef5.png) ;tente concluir ,talvez o desenvlovimento acima está no formato do seu gabarito ,se não ,post !
;tente concluir ,talvez o desenvlovimento acima está no formato do seu gabarito ,se não ,post !

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)