 por lucas7 » Seg Dez 24, 2012 18:18
por lucas7 » Seg Dez 24, 2012 18:18
Determine se a serie converge e, se convergir, encontre sua soma.
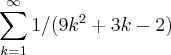
Eu sei que converge, pois fazendo o teste de mao as parcelas vao diminuindo, a soma seria 1/10 + 1/40 + 1/81...
mas nao sei como descobrir a soma, parece ser uma serie telescopica.
Agradeco muito se alguem puder me ajudar e explicar.
ps:A soma deve dar 4/7!
Abracos e feliz natal!
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por young_jedi » Seg Dez 24, 2012 20:47
por young_jedi » Seg Dez 24, 2012 20:47
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por lucas7 » Ter Dez 25, 2012 01:26
por lucas7 » Ter Dez 25, 2012 01:26
O seu resultado esta certo! eu olhei o gabarito de uma outra questao por engano, desculpe. A resposta correta eh 1/6! Muitissimo obrigado!


O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema equação de 2 grau - soma e produto
por melned » Ter Mar 10, 2009 16:17
- 1 Respostas
- 2653 Exibições
- Última mensagem por Marcampucio

Ter Mar 10, 2009 19:50
Sistemas de Equações
-
- Somatório
por ARCS » Sáb Mar 12, 2011 01:51
- 3 Respostas
- 4096 Exibições
- Última mensagem por Renato_RJ

Sáb Mar 12, 2011 03:14
Sequências
-
- Somatório
por Abelardo » Sex Abr 01, 2011 01:06
- 0 Respostas
- 1460 Exibições
- Última mensagem por Abelardo

Sex Abr 01, 2011 01:06
Álgebra Elementar
-
- Somatório
por alienante » Qua Mai 07, 2014 14:59
- 1 Respostas
- 1438 Exibições
- Última mensagem por Russman

Qua Mai 07, 2014 19:14
Álgebra Elementar
-
- Sequências e convergência
por Danilo » Qui Abr 05, 2012 23:33
- 8 Respostas
- 4348 Exibições
- Última mensagem por Danilo

Sáb Abr 14, 2012 17:33
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
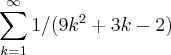


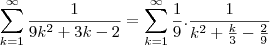
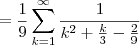
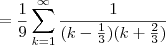
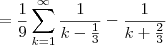
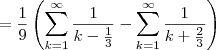
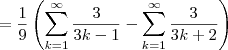
![\frac{1}{9}\left[\left(\frac{3}{2}+\frac{3}{5}+\frac{3}{8}+\frac{3}{11}\dots\right)-\left(\frac{3}{5}+\frac{3}{8}+\frac{3}{11}\dots\right)\right] \frac{1}{9}\left[\left(\frac{3}{2}+\frac{3}{5}+\frac{3}{8}+\frac{3}{11}\dots\right)-\left(\frac{3}{5}+\frac{3}{8}+\frac{3}{11}\dots\right)\right]](/latexrender/pictures/2e8cc4e1894da13fc35b4b22def3c0a4.png)
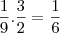




 .
.
 :
: