 por Rafael+10 » Qui Nov 22, 2012 08:52
por Rafael+10 » Qui Nov 22, 2012 08:52
Numa amostra de 140g de uma liga de metais , há 80% de ouro , 15% de prata e 5% de cobre. Quantos gramas de prata e quantos gramas de cobre devem ser adicionados a essa amostra de modo que, na nova mistura , haja 20% de prata e de 10% de cobra?
-
Rafael+10
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Nov 22, 2012 08:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Qui Nov 22, 2012 09:22
por replay » Qui Nov 22, 2012 09:22
Primeiro vamos as contas:
Ouro:
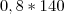
= 112g
Prata:
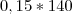
= 21g
Cobre:

= 7
O exercicio pede quantas gramas de prata e cobre devem ser adicionados para que tenha 20% do total de prata e de 10% do total de cobre.
Editado pela última vez por
replay em Qui Nov 22, 2012 10:28, em um total de 2 vezes.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Rafael+10 » Qui Nov 22, 2012 09:24
por Rafael+10 » Qui Nov 22, 2012 09:24
Mas nao eh issoo...eu achei esses valores, mas no gabarito , esta dando que deve ser adicionados 9g de cada... O.o
-
Rafael+10
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Nov 22, 2012 08:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Qui Nov 22, 2012 09:35
por replay » Qui Nov 22, 2012 09:35
Ja sei o que acontece, acontece que ignoramos o peso total ou seja:
Ele não pede que seja substituido, mas que seja adicionado, se eu adicionar 7g de cada terei que tirar 14g de ouro, ou seja, não é isso que o exercicio pede, vou fazer nova conta aqui.
Uma falta de atenção e isso ocorre.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Rafael+10 » Qui Nov 22, 2012 10:17
por Rafael+10 » Qui Nov 22, 2012 10:17
pode creer... Mas msm assim to travando aki e nao consigo resolver essa porcaria..kkkk
-
Rafael+10
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Nov 22, 2012 08:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Qui Nov 22, 2012 10:41
por replay » Qui Nov 22, 2012 10:41
Voce pode fazer por aproximação.
Você sabe que adicionar 7 aumentamos o total para 140+7
Logo temos
21/140 = 0,15 = 15%
22/141 = 0,1560 = 15,60%
23/142 = 0,1619 = 16,19%
...
29/148 = 0,1959
30/149 = 0,2013 = 20,13% = Logo resposta mais aproximada é aumentar 9 na prata.
Se fizer isso no cobre temos:
7+9= 16 ... Como eu aumento 9 no cobre aumenta 9 no total sendo:
16/158 = 0,1012 ou 10% aproximado.
Editado pela última vez por
replay em Qui Nov 22, 2012 11:18, em um total de 3 vezes.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Rafael+10 » Qui Nov 22, 2012 11:17
por Rafael+10 » Qui Nov 22, 2012 11:17
valeu

...eu consegui fazer ...kkkkk

-
Rafael+10
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Nov 22, 2012 08:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Qui Nov 22, 2012 13:21
por replay » Qui Nov 22, 2012 13:21
Qual outra conta você utilizou ? Fiquei curioso xD
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Porcentagem] Fração mista e porcentagem
por Mayra Luna » Ter Fev 26, 2013 20:58
- 2 Respostas
- 4580 Exibições
- Última mensagem por Mayra Luna

Ter Fev 26, 2013 23:41
Álgebra Elementar
-
- Porcentagem - Porcentagem com minutos
por marcorrer » Qua Abr 04, 2012 13:52
- 6 Respostas
- 7908 Exibições
- Última mensagem por marcorrer

Seg Abr 09, 2012 16:25
Álgebra Elementar
-
- Porcentagem
por Danilo Dias Vilela » Qui Set 10, 2009 22:31
- 1 Respostas
- 3750 Exibições
- Última mensagem por Molina

Sex Set 11, 2009 14:22
Matemática Financeira
-
- Porcentagem
por Danilo Dias Vilela » Sex Set 11, 2009 18:09
- 2 Respostas
- 3682 Exibições
- Última mensagem por Danilo Dias Vilela

Sex Set 11, 2009 21:17
Matemática Financeira
-
- Porcentagem
por matematicando » Ter Set 15, 2009 12:52
- 0 Respostas
- 2919 Exibições
- Última mensagem por matematicando

Ter Set 15, 2009 12:52
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



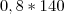 = 112g
= 112g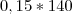 = 21g
= 21g = 7
= 7




 ...eu consegui fazer ...kkkkk
...eu consegui fazer ...kkkkk 




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.