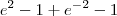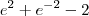por Dan » Ter Set 15, 2009 17:19
por Dan » Ter Set 15, 2009 17:19
Oi gente. Estou aprendendo integrais definidas e gostaria de saber se a resolução da seguinte integral está correta. Ela é bem simples, mas eu fico em dúvida quanto aos sinais e obviamente não tenho a resposta:
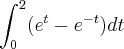
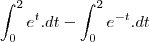
A minha principal dúvida é nesses sinais:
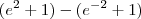
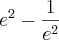
Não penso que seja isso... Até porque nesse exemplo o
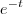
não foi corretamente integrado. Refiz agora e deu:
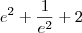
Eu me confundi principalmente pois
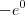
é igual a 1, e não a -1.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Ter Set 15, 2009 18:57
por Molina » Ter Set 15, 2009 18:57
Dan escreveu: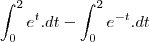
A minha principal dúvida é nesses sinais:
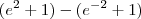
Na verdade
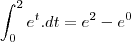
e
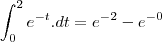
Você está colocando o sinal de mais na hora que faz a intergral nos limites, e é
menos.
Juntando tudo:
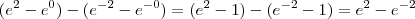

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Dan » Qua Set 16, 2009 09:51
por Dan » Qua Set 16, 2009 09:51
Olá molina.
Quer dizer que quando temos
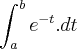
a integral disso é só
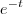
?
Eu tava achando que tinha que derivar o -t, que daria -1. Tem que ou não tem que fazer isso?
Então só deve ser feita essa derivação em casos como
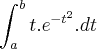
onde temos uma variável multiplicando?
Acontece que quando temos a integral indefinida
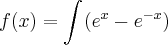
o resultado disso dá
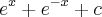
.
Ou seja, quando derivamos esse -x, o sinal do e muda. Isso não acontece só porque a integral é definida? Porque o sinal do e não muda se o expoente é negativo?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Qua Set 16, 2009 14:26
por Molina » Qua Set 16, 2009 14:26
Desculpe-me. Realmente me confundi na segunda integral. Corrigindo:
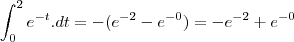
Abraços!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Dan » Qua Set 16, 2009 15:08
por Dan » Qua Set 16, 2009 15:08
Esses sinais tão de matar mesmo...
Olha só, eu tava refazendo agora e achei o seguinte:
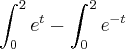
Isso dá:
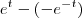
(só pra visualizar)
Agora:
![e^2 - e^0-[-e^{-2}-(-e^0)] e^2 - e^0-[-e^{-2}-(-e^0)]](/latexrender/pictures/71342f9b3375e0bedfcf44aeea392393.png)
Espero que esse raciocínio que eu usei esteja correto, porque se for assim, imagino eu que o resultado seja o seguinte:
![e^2 - 1-[-e^{-2}-(1)] e^2 - 1-[-e^{-2}-(1)]](/latexrender/pictures/c2a1dff86c7f10ab3510c2e8e9cf1439.png)
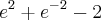
Só que eu ainda não estou certo da resolução, pois não sei se esse 1 fica positivo ou negativo. Eu deixei ele negativo aí pois segui a lógica que qualquer número, mesmo negativo, quando elevado na 0 dá 1 positivo (com o sinal daí ele volta a ficar negativo).
Essa idéia está certa?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Qua Set 16, 2009 21:44
por Molina » Qua Set 16, 2009 21:44
Dan escreveu:Esses sinais tão de matar mesmo...
Olha só, eu tava refazendo agora e achei o seguinte:
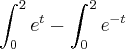
Isso dá:
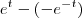
(só pra visualizar)
Agora:
![e^2 - e^0-[-e^{-2}-(-e^0)] e^2 - e^0-[-e^{-2}-(-e^0)]](/latexrender/pictures/71342f9b3375e0bedfcf44aeea392393.png)
Espero que esse raciocínio que eu usei esteja correto, porque se for assim, imagino eu que o resultado seja o seguinte:
![e^2 - 1-[-e^{-2}-(1)] e^2 - 1-[-e^{-2}-(1)]](/latexrender/pictures/c2a1dff86c7f10ab3510c2e8e9cf1439.png)
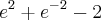
Só que eu ainda não estou certo da resolução, pois não sei se esse 1 fica positivo ou negativo. Eu deixei ele negativo aí pois segui a lógica que qualquer número, mesmo negativo, quando elevado na 0 dá 1 positivo (com o sinal daí ele volta a ficar negativo).
Essa idéia está certa?
Olá, amigo.
Lembre-se que

e
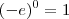
Então desta passagem:
![e^2 - e^0-[-e^{-2}-(-e^0)] e^2 - e^0-[-e^{-2}-(-e^0)]](/latexrender/pictures/71342f9b3375e0bedfcf44aeea392393.png)
temos que:
![e^2 - 1-[-e^{-2}-(-1)] e^2 - 1-[-e^{-2}-(-1)]](/latexrender/pictures/4897e5713a76563f26880a97b98ac945.png)
![e^2 - 1-[-e^{-2}+1] e^2 - 1-[-e^{-2}+1]](/latexrender/pictures/62ab46f2b357304ea5650a6bb4a3d4b0.png)
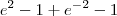
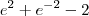
Que no fim das contas deu a mesma coisa que você tinha colocado.
Só naquela primeira passagem que faltou o sinal de negativo na frente.
Mas acho que é isso mesmo.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4623 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4591 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4349 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2852 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2880 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
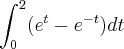
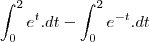
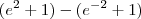
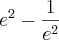
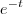 não foi corretamente integrado. Refiz agora e deu:
não foi corretamente integrado. Refiz agora e deu: 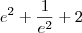
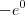 é igual a 1, e não a -1.
é igual a 1, e não a -1.
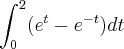
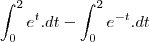
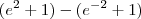
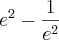
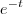 não foi corretamente integrado. Refiz agora e deu:
não foi corretamente integrado. Refiz agora e deu: 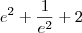
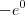 é igual a 1, e não a -1.
é igual a 1, e não a -1.
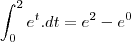
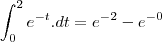
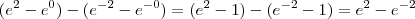


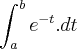 a integral disso é só
a integral disso é só 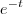 ?
?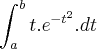 onde temos uma variável multiplicando?
onde temos uma variável multiplicando?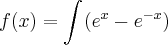 o resultado disso dá
o resultado disso dá 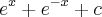 .
.
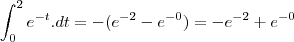

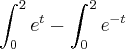
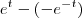 (só pra visualizar)
(só pra visualizar)![e^2 - e^0-[-e^{-2}-(-e^0)] e^2 - e^0-[-e^{-2}-(-e^0)]](/latexrender/pictures/71342f9b3375e0bedfcf44aeea392393.png)
![e^2 - 1-[-e^{-2}-(1)] e^2 - 1-[-e^{-2}-(1)]](/latexrender/pictures/c2a1dff86c7f10ab3510c2e8e9cf1439.png)
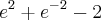

(só pra visualizar)
 e
e 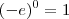
![e^2 - e^0-[-e^{-2}-(-e^0)] e^2 - e^0-[-e^{-2}-(-e^0)]](/latexrender/pictures/71342f9b3375e0bedfcf44aeea392393.png) temos que:
temos que:![e^2 - 1-[-e^{-2}-(-1)] e^2 - 1-[-e^{-2}-(-1)]](/latexrender/pictures/4897e5713a76563f26880a97b98ac945.png)
![e^2 - 1-[-e^{-2}+1] e^2 - 1-[-e^{-2}+1]](/latexrender/pictures/62ab46f2b357304ea5650a6bb4a3d4b0.png)