Não faz sentido porque você somou a mesma equação a ela. Note que o resultado que você chegou, que é

, é simplesmente um múltiplo da equação do plano original. Quando você substituiu
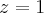
, você fez a interseção do plano com o plano
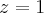
, que é paralelo ao plano
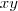
. Daí você encontrou a reta que é a interseção destes dois planos.
Em outras palavras, você resolveu um problema diferente do enunciado. Não tente fixar um método de resolução para tudo, é caminho certo para falhar.
Para começar, eu faria o mesmo que fez: substituir e ver o que encontra. Como não há erros na álgebra e você viu que é independente do parâmetro, deveria ter pensado um pouco e percebido que a reta estava contida no plano.
Se você chegasse numa impossibilidade, como
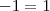
, então a reta não teria interseção com o plano.
Por último, se encontrasse um valor único para o parâmetro, como

, então a interseção seria um único ponto e você substituiria na equação da reta para encontrar este ponto.
 .
.
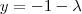
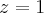
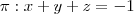
 , ficando:
, ficando:
 vai se cortar... e não vou conseguir descobrir seu valor desta forma.
vai se cortar... e não vou conseguir descobrir seu valor desta forma.

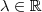 , e vemos que o vetor normal ao plano, que é
, e vemos que o vetor normal ao plano, que é 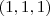 , é ortogonal ao vetor diretor da reta, que é
, é ortogonal ao vetor diretor da reta, que é 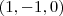 .
.

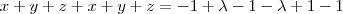


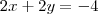

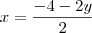

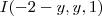
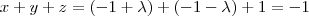 , que é justamente a equação do plano. A conclusão é que a reta está contida no plano.
, que é justamente a equação do plano. A conclusão é que a reta está contida no plano. , é simplesmente um múltiplo da equação do plano original. Quando você substituiu
, é simplesmente um múltiplo da equação do plano original. Quando você substituiu 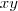 . Daí você encontrou a reta que é a interseção destes dois planos.
. Daí você encontrou a reta que é a interseção destes dois planos.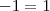 , então a reta não teria interseção com o plano.
, então a reta não teria interseção com o plano.  , então a interseção seria um único ponto e você substituiria na equação da reta para encontrar este ponto.
, então a interseção seria um único ponto e você substituiria na equação da reta para encontrar este ponto.
 .
.
 :
: