 por MrJuniorFerr » Dom Out 14, 2012 17:50
por MrJuniorFerr » Dom Out 14, 2012 17:50
Boa tarde a todos.
Estou com dúvida no seguinte exercício:
Obtenha a interseção da reta r com o plano  .
.reta r:

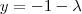
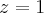
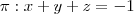
Eu tentei resolver da seguinte forma:
Os valores de x, y, e z de r, eu os substituí na na equação

, ficando:

Mas como podem ver, o

vai se cortar... e não vou conseguir descobrir seu valor desta forma.
Como eu poderia resolver este sistema?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Dom Out 14, 2012 18:27
por MarceloFantini » Dom Out 14, 2012 18:27
Isto provavelmente significa que a reta está contida no plano.
A igualdade será satisfeita para qualquer
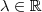
, e vemos que o vetor normal ao plano, que é
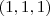
, é ortogonal ao vetor diretor da reta, que é
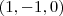
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Dom Out 14, 2012 18:53
por MrJuniorFerr » Dom Out 14, 2012 18:53
MarceloFantini escreveu:Isto provavelmente significa que a reta está contida no plano.
A igualdade será satisfeita para qualquer
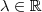
, e vemos que o vetor normal ao plano, que é
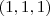
, é ortogonal ao vetor diretor da reta, que é
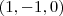
.
Se nesse caso, a reta está contida no plano, a interseção da reta e o plano é a própria reta?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Dom Out 14, 2012 18:56
por MarceloFantini » Dom Out 14, 2012 18:56
Sim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Dom Out 14, 2012 19:10
por MrJuniorFerr » Dom Out 14, 2012 19:10
Marcelo, antes de você me responder, eu tinha conseguido resolver o sistema... só que não tenho certeza q está certo, olhe:
Eu somei todas as equações e obtive:
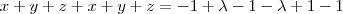
e cheguei em:

como z=1,

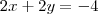

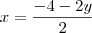

Sabendo disso, o ponto de interseção é:
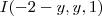
Se você não me falasse, eu iria resolver dessa forma, e achar que a interseção dessa reta e o plano, seria um ponto...
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Dom Out 14, 2012 19:26
por MarceloFantini » Dom Out 14, 2012 19:26
Sua resolução não faz sentido. A interseção de uma reta e um plano só pode ser uma de três possibilidades: nada, um ponto ou uma reta, que é o caso em que a reta está contida no plano.
Note que se você somasse apenas as equações da reta, perceberia que
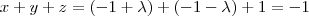
, que é justamente a equação do plano. A conclusão é que a reta está contida no plano.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Dom Out 14, 2012 19:42
por MrJuniorFerr » Dom Out 14, 2012 19:42
Por qual motivo a minha resolução não faz sentido? Não pode somar todas as equações como eu somei?
Se a professora colocasse um exercício desse tipo na prova, eu teria que avaliar então se o vetor diretor da reta é perpendicular ao vetor normal do plano para qualquer das três possibilidades que você citou?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Dom Out 14, 2012 19:53
por MarceloFantini » Dom Out 14, 2012 19:53
Não faz sentido porque você somou a mesma equação a ela. Note que o resultado que você chegou, que é

, é simplesmente um múltiplo da equação do plano original. Quando você substituiu
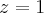
, você fez a interseção do plano com o plano
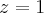
, que é paralelo ao plano
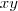
. Daí você encontrou a reta que é a interseção destes dois planos.
Em outras palavras, você resolveu um problema diferente do enunciado. Não tente fixar um método de resolução para tudo, é caminho certo para falhar.
Para começar, eu faria o mesmo que fez: substituir e ver o que encontra. Como não há erros na álgebra e você viu que é independente do parâmetro, deveria ter pensado um pouco e percebido que a reta estava contida no plano.
Se você chegasse numa impossibilidade, como
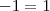
, então a reta não teria interseção com o plano.
Por último, se encontrasse um valor único para o parâmetro, como

, então a interseção seria um único ponto e você substituiria na equação da reta para encontrar este ponto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MrJuniorFerr » Dom Out 14, 2012 22:35
por MrJuniorFerr » Dom Out 14, 2012 22:35
Entendi Marcelo, vou começar a prestar mais atenção nos detalhes. Aprendi com você que nada acontece por acaso, ou seja, para todo acontecimento há uma causa. Obrigado.
Na resolução deste exercício, posso explicar a minha conclusão da reta estar contida no plano a partir do parâmetro

se cortar na substituição?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MarceloFantini » Dom Out 14, 2012 22:38
por MarceloFantini » Dom Out 14, 2012 22:38
Sim, mostre que ela satisfaz a equação do plano. Pode fazer isto substituindo ou somando (são processos equivalentes).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Interseção de reta e plano] Dúvida exerc. 2
por MrJuniorFerr » Seg Out 15, 2012 00:35
- 3 Respostas
- 2197 Exibições
- Última mensagem por MarceloFantini

Seg Out 15, 2012 08:13
Geometria Analítica
-
- interseção,área e reta dúvida exercício
por igor44 » Seg Out 31, 2011 21:20
- 1 Respostas
- 2137 Exibições
- Última mensagem por procyon

Ter Nov 01, 2011 00:57
Geometria Analítica
-
- [Dúvida reta e plano]
por Andresa_s » Qua Ago 01, 2012 13:02
- 1 Respostas
- 1606 Exibições
- Última mensagem por MarceloFantini

Qua Ago 01, 2012 21:07
Geometria Espacial
-
- [Ângulo - reta e plano] Dúvida exercício
por MrJuniorFerr » Sex Out 12, 2012 11:51
- 6 Respostas
- 4626 Exibições
- Última mensagem por MarceloFantini

Sex Out 12, 2012 20:18
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14964 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.
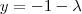
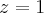
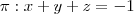
 , ficando:
, ficando:
 vai se cortar... e não vou conseguir descobrir seu valor desta forma.
vai se cortar... e não vou conseguir descobrir seu valor desta forma.

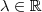 , e vemos que o vetor normal ao plano, que é
, e vemos que o vetor normal ao plano, que é 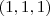 , é ortogonal ao vetor diretor da reta, que é
, é ortogonal ao vetor diretor da reta, que é 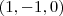 .
.

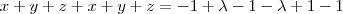


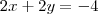

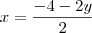

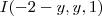
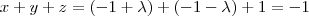 , que é justamente a equação do plano. A conclusão é que a reta está contida no plano.
, que é justamente a equação do plano. A conclusão é que a reta está contida no plano. , é simplesmente um múltiplo da equação do plano original. Quando você substituiu
, é simplesmente um múltiplo da equação do plano original. Quando você substituiu 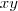 . Daí você encontrou a reta que é a interseção destes dois planos.
. Daí você encontrou a reta que é a interseção destes dois planos.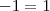 , então a reta não teria interseção com o plano.
, então a reta não teria interseção com o plano.  , então a interseção seria um único ponto e você substituiria na equação da reta para encontrar este ponto.
, então a interseção seria um único ponto e você substituiria na equação da reta para encontrar este ponto.




