 por iarapassos » Seg Set 03, 2012 22:26
por iarapassos » Seg Set 03, 2012 22:26
Seja o ponto
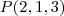
, determine seu simétrico em relação:
à reta

coloquei na matriz pq não encontrei outro símbolo mais adequado (que seria uma única chave)
ao plano:

Me dê uma luz!
Não sei como fazer esta questão!
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Qua Set 05, 2012 17:02
por LuizAquino » Qua Set 05, 2012 17:02
iarapassos escreveu:Seja o ponto
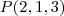
, determine seu simétrico em relação:
à reta

coloquei na matriz pq não encontrei outro símbolo mais adequado (que seria uma única chave)
ao plano:

Me dê uma luz!
Não sei como fazer esta questão!
Em relação ao símbolo "chave única", use o seguinte código:
- Código: Selecionar todos
[tex]
\begin{cases}
x = 1 - 2t \\
y = t \\
z = 2 + t
\end{cases}
[/tex]
O resultado será:

Em relação ao exercício, a primeira coisa que você precisa saber é o que significa o "simétrico" de um ponto P em relação a uma reta (ou a um plano). Você sabe o que isso significa?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ponto simétrico
por sinuca147 » Seg Mai 25, 2009 09:40
- 3 Respostas
- 32325 Exibições
- Última mensagem por gustavoluiss

Seg Jan 03, 2011 02:03
Álgebra Elementar
-
- Simetrico de um ponto
por izabela » Seg Mai 23, 2011 21:13
- 0 Respostas
- 1795 Exibições
- Última mensagem por izabela

Seg Mai 23, 2011 21:13
Geometria Analítica
-
- Ponto Simétrico
por Claudin » Qui Abr 05, 2012 19:16
- 3 Respostas
- 3190 Exibições
- Última mensagem por Claudin

Sáb Abr 07, 2012 10:32
Geometria Analítica
-
- [PONTO SIMÉTRICO]
por renan_a » Sáb Out 20, 2012 22:00
- 3 Respostas
- 9544 Exibições
- Última mensagem por renan_a

Dom Out 21, 2012 15:49
Geometria Analítica
-
- Ponto Simétrico
por nataliaknot » Sáb Mar 08, 2014 21:23
- 2 Respostas
- 2234 Exibições
- Última mensagem por nataliaknot

Dom Mar 09, 2014 11:46
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
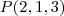 , determine seu simétrico em relação:
, determine seu simétrico em relação: coloquei na matriz pq não encontrei outro símbolo mais adequado (que seria uma única chave)
coloquei na matriz pq não encontrei outro símbolo mais adequado (que seria uma única chave)

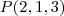 , determine seu simétrico em relação:
, determine seu simétrico em relação: coloquei na matriz pq não encontrei outro símbolo mais adequado (que seria uma única chave)
coloquei na matriz pq não encontrei outro símbolo mais adequado (que seria uma única chave)

, determine seu simétrico em relação:
coloquei na matriz pq não encontrei outro símbolo mais adequado (que seria uma única chave)



 .
.
 :
: