Scorpion tinha uma mochila com cabeças e encontrou um amigo a quem deu metade das cabeças que tinha e mais
meia cabeça. Posteriormente, encontrou outro amigo a quem deu igualmente metade das cabeças que lhe
restaram, mais meia cabeça. Por fim, encontrou um terceiro amigo e deu-lhe novamente metade das cabeças
que lhe sobraram e mais meia cabeça, ficando sem nenhuma cabeça. Quantas cabeças Scorpion tinha antes de
encontrar o primeiro amigo ?
Alguem consegue dar um FINISH nessa questão ?



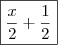 cabeças;
cabeças;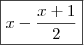 , ou seja:
, ou seja: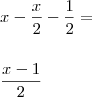
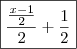 cabeças, ou seja:
cabeças, ou seja: 
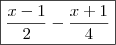 , isto é:
, isto é: 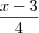
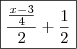 cabeças, ou seja:
cabeças, ou seja: 
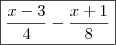 , isto é:
, isto é: 
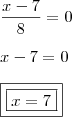


 .
.
 :
: