 por JKS » Qui Ago 23, 2012 19:07
por JKS » Qui Ago 23, 2012 19:07
Preciso de ajuda, desde já agradeço ..
Considere a função y= f(x) definida por :
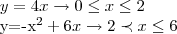
a) Para que valores de x temos f(x) = 5 ?
Resposta :

e 5
Não entendi como ele achou o

-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Ago 23, 2012 20:19
por MarceloFantini » Qui Ago 23, 2012 20:19
Para descobrir os valores de

tais que

, analisemos a função em cada intervalo em que está definida. Primeiro, se
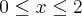
temos
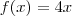
. Daí, se

então
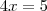
de onde
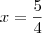
, que está no intervalo
![[0,2] [0,2]](/latexrender/pictures/70fd3f388413505934da60b43afc4088.png)
. Já encontramos uma solução.
Analisemos agora no outro intervalo. Para
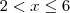
temos
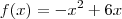
, daí
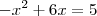
e
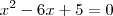
. Suas raízes são

e

. Como

não está no intervalo, segue que a outra solução é

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JKS » Sex Ago 24, 2012 12:44
por JKS » Sex Ago 24, 2012 12:44
Concordo com você.. a reposta tem que ser

.. o gabarito está errado, não tem como ser

..
Muito Obrigadaa.. está me ajudando muitoo, não tem como retribuir a excelente iniciativa de vocês .. muito Obrigada mesmo ..
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
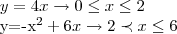
 e 5
e 5 

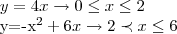
 e 5
e 5 

 tais que
tais que  , analisemos a função em cada intervalo em que está definida. Primeiro, se
, analisemos a função em cada intervalo em que está definida. Primeiro, se 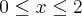 temos
temos 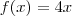 . Daí, se
. Daí, se  então
então 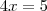 de onde
de onde 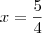 , que está no intervalo
, que está no intervalo ![[0,2] [0,2]](/latexrender/pictures/70fd3f388413505934da60b43afc4088.png) . Já encontramos uma solução.
. Já encontramos uma solução.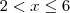 temos
temos 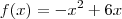 , daí
, daí 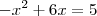 e
e 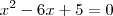 . Suas raízes são
. Suas raízes são  e
e  . Como
. Como  não está no intervalo, segue que a outra solução é
não está no intervalo, segue que a outra solução é  .
.

 .. o gabarito está errado, não tem como ser
.. o gabarito está errado, não tem como ser  ..
.. 

 .
.
 :
: