 por JKS » Qui Ago 23, 2012 19:07
por JKS » Qui Ago 23, 2012 19:07
Preciso de ajuda, desde já agradeço ..
Considere a função y= f(x) definida por :
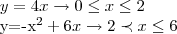
a) Para que valores de x temos f(x) = 5 ?
Resposta :

e 5
Não entendi como ele achou o

-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Ago 23, 2012 20:19
por MarceloFantini » Qui Ago 23, 2012 20:19
Para descobrir os valores de

tais que

, analisemos a função em cada intervalo em que está definida. Primeiro, se
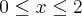
temos
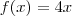
. Daí, se

então
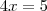
de onde
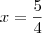
, que está no intervalo
![[0,2] [0,2]](/latexrender/pictures/70fd3f388413505934da60b43afc4088.png)
. Já encontramos uma solução.
Analisemos agora no outro intervalo. Para
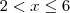
temos
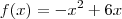
, daí
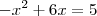
e
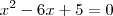
. Suas raízes são

e

. Como

não está no intervalo, segue que a outra solução é

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JKS » Sex Ago 24, 2012 12:44
por JKS » Sex Ago 24, 2012 12:44
Concordo com você.. a reposta tem que ser

.. o gabarito está errado, não tem como ser

..
Muito Obrigadaa.. está me ajudando muitoo, não tem como retribuir a excelente iniciativa de vocês .. muito Obrigada mesmo ..
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
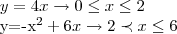
 e 5
e 5 

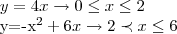
 e 5
e 5 

 tais que
tais que  , analisemos a função em cada intervalo em que está definida. Primeiro, se
, analisemos a função em cada intervalo em que está definida. Primeiro, se 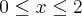 temos
temos 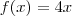 . Daí, se
. Daí, se  então
então 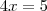 de onde
de onde 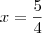 , que está no intervalo
, que está no intervalo ![[0,2] [0,2]](/latexrender/pictures/70fd3f388413505934da60b43afc4088.png) . Já encontramos uma solução.
. Já encontramos uma solução.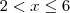 temos
temos 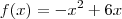 , daí
, daí 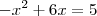 e
e 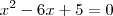 . Suas raízes são
. Suas raízes são  e
e  . Como
. Como  não está no intervalo, segue que a outra solução é
não está no intervalo, segue que a outra solução é  .
.

 .. o gabarito está errado, não tem como ser
.. o gabarito está errado, não tem como ser  ..
.. 


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.