 por Claudin » Qui Jul 05, 2012 19:57
por Claudin » Qui Jul 05, 2012 19:57
Determine a equação do plano que passa pelos pontos A(1,1,-1); B(-2,-2,2); C(1,-1,2)
Não sei como iniciar esse exercício, alguma dica?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Qui Jul 05, 2012 21:50
por Russman » Qui Jul 05, 2012 21:50
Qual a forma geral de um plano?
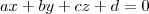
.
Monte um sistema e determine os valores
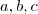
e
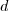
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Sex Jul 06, 2012 11:04
por Claudin » Sex Jul 06, 2012 11:04
Montei o sistema:
a + b - c +d = 0
-2a -2b +2c +d =0
a -b +2c +d=0
Porém, se escalonando não cheguei a nenhum resultado, e então continuo com a duvida.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Sex Jul 06, 2012 15:45
por Russman » Sex Jul 06, 2012 15:45
Se este meio não está claro pra você, tente por veotres. Você sabe trabalhar com vetores?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Sex Jul 06, 2012 16:24
por Claudin » Sex Jul 06, 2012 16:24
Essa questão está me confundindo, não sei como resolvê-la, se tiver como explicar melhor, agradeço.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Sex Jul 06, 2012 16:27
por Russman » Sex Jul 06, 2012 16:27
Proceda da mesma forma que eu te expliquei no outro tópico. Só que agora você deve tomar os vetores

e
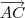
.
Com isto, use o vetor normal
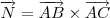
e o ponto
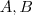
ou

para determinar o plano!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Sex Jul 06, 2012 16:28
por Claudin » Sex Jul 06, 2012 16:28
Vou refazer, qualquer duvida eu volto a perguntar. Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Jul 06, 2012 16:30
por LuizAquino » Sex Jul 06, 2012 16:30
Claudin escreveu:Determine a equação do plano que passa pelos pontos A(1,1,-1); B(-2,-2,2); C(1,-1,2)
Não sei como iniciar esse exercício, alguma dica?
Claudin escreveu:Essa questão está me confundindo, não sei como resolvê-la, se tiver como explicar melhor, agradeço.
Eu gostaria de recomendar que você assista a videoaula "14. Geometria Analítica - Equações do Plano". Nela há uma exemplo análogo a esse exercício. Essa videoaula está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sex Jul 06, 2012 16:39
por Claudin » Sex Jul 06, 2012 16:39
Obrigado pela vídeo-aula Luiz Aquino, mas a explicação do Russman já sanou minha dúvida.
Vídeo-aula sempre ajuda mas como aqui é um fórum onde pessoas trocam conhecimentos, acho eu que seria melhor explicar os tópicos e se possível reforçar a explicação com o auxílio da vídeo-aula, pois somente a vídeo-aula as vezes não ajudará tanto como a troca de informações dos frequentadores do fórum.
Obrigado

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Jul 06, 2012 16:49
por LuizAquino » Sex Jul 06, 2012 16:49
Claudin escreveu:Vídeo-aula sempre ajuda mas como aqui é um fórum onde pessoas trocam conhecimentos, acho eu que seria melhor explicar os tópicos e se possível reforçar a explicação com o auxílio da vídeo-aula, pois somente a vídeo-aula as vezes não ajudará tanto como a troca de informações dos frequentadores do fórum.
Prezado Claudin,
Na referida videoaula há um exemplo
resolvido que é inteiramente análogo ao exercício postado por você.
Se lá está
resolvido, então não vejo como a videoaula "não ajudaria" nesse caso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sex Jul 06, 2012 16:55
por Claudin » Sex Jul 06, 2012 16:55
Em momento algum eu me referi que não ajudaria, pelo contrário disse que a vídeo-aula poderia servir como reforço após a explicação e tal, mas dei somente um exemplo, tendo em vista que, a discussão em um outro tópico falando sobre isso, sobre como estão postando as dúvidas e como proceder, então só deixei minha opinião, mas respeito a sua, e em momento algum disse que sua vídeo-aula não serviria nesse caso.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sex Jul 06, 2012 17:00
por LuizAquino » Sex Jul 06, 2012 17:00
Claudin escreveu:Em momento algum eu me referi que não ajudaria, pelo contrário disse que a vídeo-aula poderia servir como reforço após a explicação e tal, mas dei somente um exemplo, tendo em vista que, a discussão em um outro tópico falando sobre isso, sobre como estão postando as dúvidas e como proceder, então só deixei minha opinião, mas respeito a sua, e em momento algum disse que sua vídeo-aula não serviria nesse caso.

Nesse caso, seria interessante que você também deixasse a sua opinião lá nesse "outro tópico":
Entender as Comunidades de Entre-ajudaviewtopic.php?f=134&t=8774
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Sáb Jul 07, 2012 02:22
por Claudin » Sáb Jul 07, 2012 02:22
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Parábola]Determinar vértice de parábola (Urgente!)
por migvas99 » Seg Out 08, 2012 14:37
- 1 Respostas
- 2732 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 17:09
Funções
-
- [Parábola] Encontrando o ponto na parábola
por Ana_Rodrigues » Ter Nov 22, 2011 20:44
- 1 Respostas
- 4887 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 21:38
Geometria Analítica
-
- Parábola
por flavio2010 » Sáb Jul 17, 2010 19:11
- 1 Respostas
- 1933 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 22:20
Funções
-
- Parábola
por flavio2010 » Dom Jul 18, 2010 19:42
- 1 Respostas
- 1824 Exibições
- Última mensagem por Tom

Dom Jul 18, 2010 23:31
Funções
-
- Parábola
por flavio2010 » Sex Jul 23, 2010 19:16
- 1 Respostas
- 1930 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 24, 2010 01:40
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



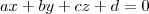 .
.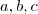 e
e 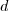 .
.



 e
e 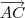 .
.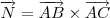 e o ponto
e o ponto 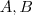 ou
ou  para determinar o plano!
para determinar o plano!














